GUM versus Exact Uncertainty of sin(x) and cos(x) When x Is Normally Distributed

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
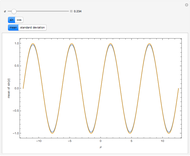
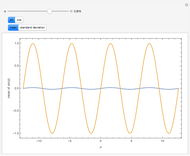
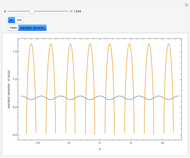
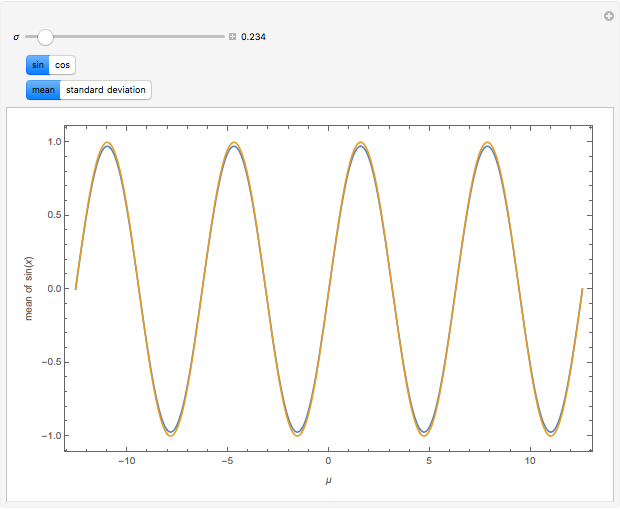
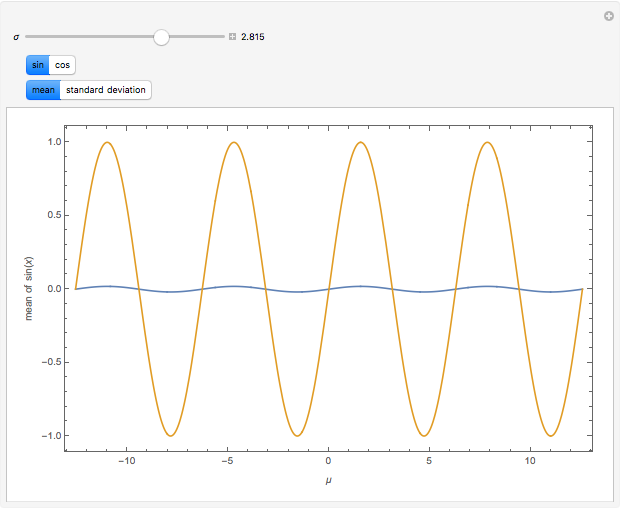
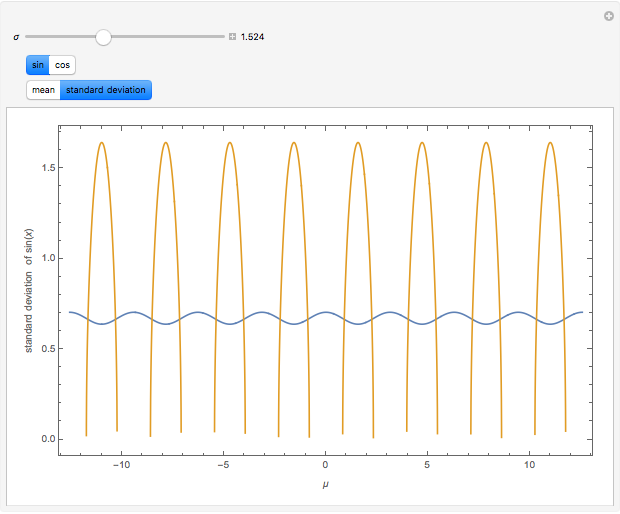
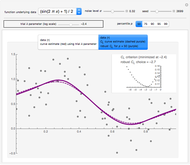
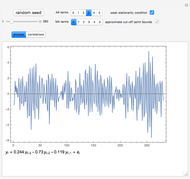
The mean and standard deviation of 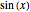 and
and 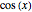 , when
, when  follows the normal distribution with mean
follows the normal distribution with mean  and standard deviation
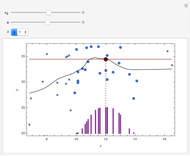
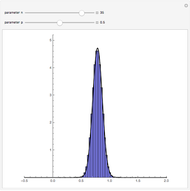
and standard deviation  , are shown on four plots to compare the approximate and exact solutions. The red curve is an approximation calculated by formulas given in GUM (Guide to Uncertainty in Measurement). The blue curve is exact, as calculated by Mathematica 8. The approximate means are independent of
, are shown on four plots to compare the approximate and exact solutions. The red curve is an approximation calculated by formulas given in GUM (Guide to Uncertainty in Measurement). The blue curve is exact, as calculated by Mathematica 8. The approximate means are independent of  and all the approximations are better for small values of
and all the approximations are better for small values of  .
.
Contributed by: M. D. Mikhailov and V. Y. Aibe (June 2012)
(Instituto Nacional de Metrologia, Qualidade e Tecnologia (Inmetro), Brazil)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The approximate means and standard deviations of 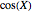 and
and 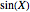 , where
, where 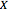 is a normal random variable with mean
is a normal random variable with mean  and standard deviation
and standard deviation  are
are
 ,
,
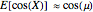 ,
,
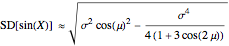 ,
,
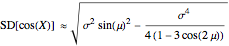 .
.
The exact means and standard deviations as calculated by Mathematica 8 are
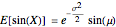 ,
,
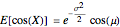 ,
,
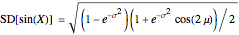 ,
,
 .
.
Reference
[1] "Evaluation of Measurement Data—Guide to the Expression of Uncertainty in Measurement." BIPM. (Sept 2008) www.bipm.org/utils/common/documents/jcgm/JCGM_100_ 2008_E.pdf.
Permanent Citation