Hierarchical Zonotopal Spaces

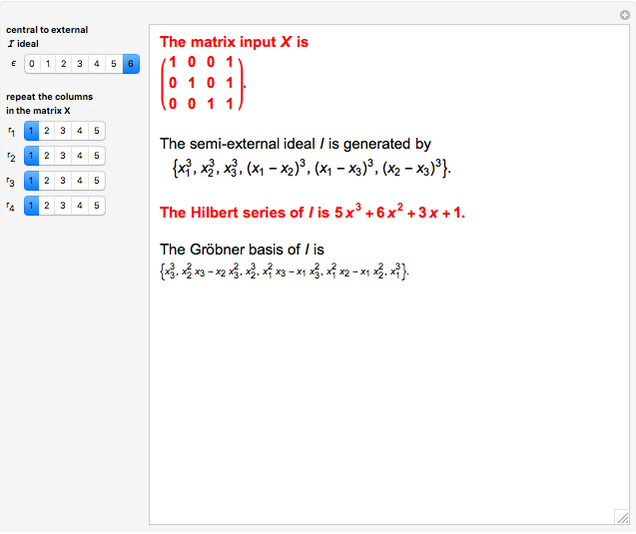
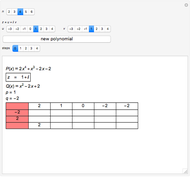
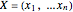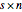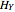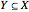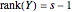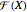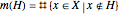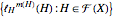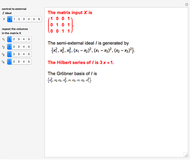
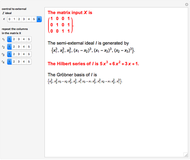
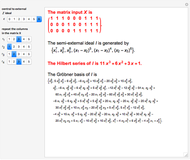
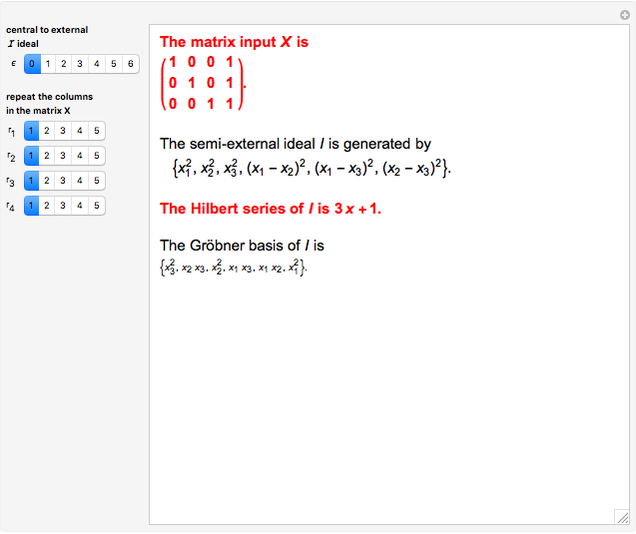
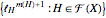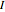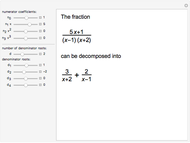
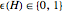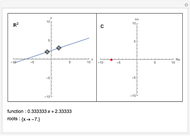
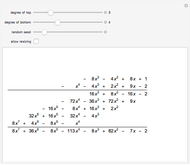
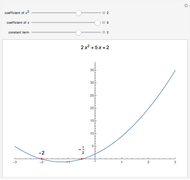
Suppose is an matrix. Let denote the hyperplane generated by a submatrix , with and denote by the set of all . The normal to a hyperplane is denoted by ; let . Then the central and the external ideals are generated by and , respectively. The semi-external ideal is generated by , where . The kernel of the central and external ideals are zonotopal spaces, while the kernel of the semi-external ideal 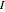is a hierarchical zonotopal space. This Demonstration shows the Hilbert series and Gröbner basis of the semi-external ideal .