Polynomial Roots in the Complex Plane
Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
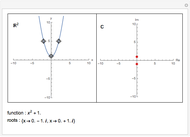
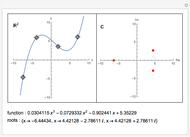
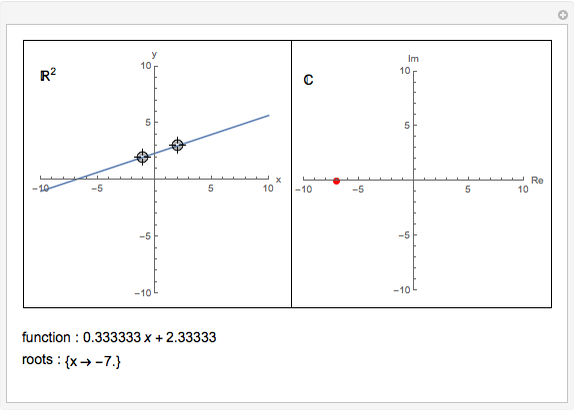
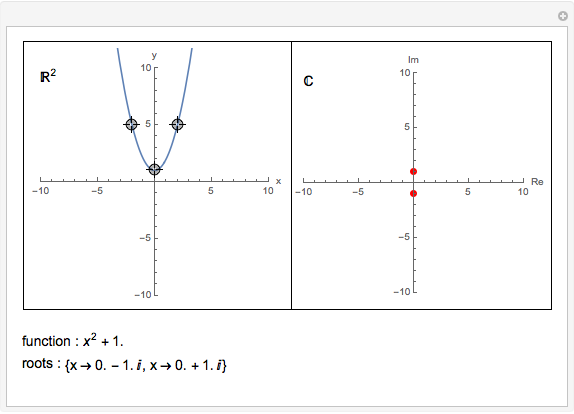
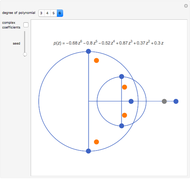
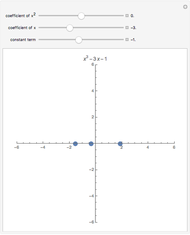
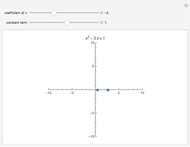
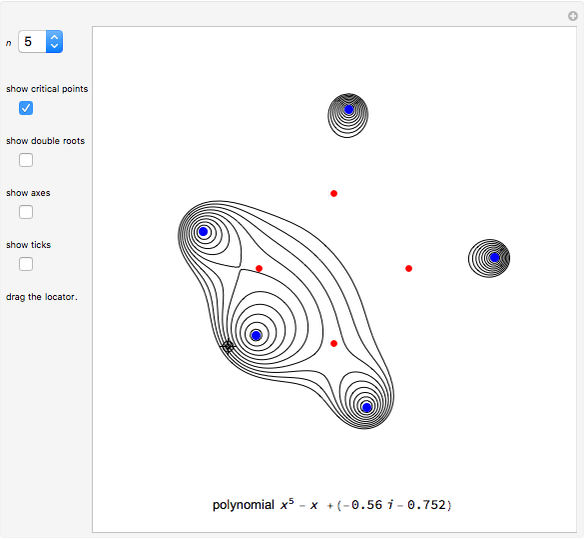
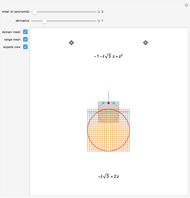
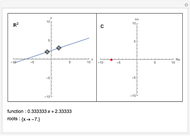
This is an illustration of the fundamental theorem of algebra. Roots of a polynomial can be visualized as points in the complex plane ℂ. This Demonstration plots a polynomial in the real 
, 
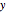plane 
and the corresponding roots in ℂ.
Contributed by: Faisal Mohamed (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
detailSectionParagraphPermanent Citation
"Polynomial Roots in the Complex Plane"
http://demonstrations.wolfram.com/PolynomialRootsInTheComplexPlane/
Wolfram Demonstrations Project
Published: March 7 2011
Ruffini-Horner Algorithm for Complex Arguments
Izidor Hafner
The Eneström-Kakeya Bounds for Roots of a Polynomial with Positive Coefficients
Andrzej Kozlowski
Roots of a Polynomial with Complex Coefficients
Izidor Hafner
Jensen's Disks
Michael Schreiber
Perturbing the Constant Coefficient of a Complex Polynomial
Izidor Hafner
Rational Roots of a Polynomial
Izidor Hafner
Sliding the Roots of Cubics
Robert Baillie
Sliding the Roots of Quadratics
Robert Baillie
How the Roots of a Polynomial Depend on Its Constant Coefficient
Izidor Hafner
Complex Roots of a Polynomial and Its Derivative
Michael Schreiber
-
Tile Murals
Faisal Mohamed -
Polynomial Roots in the Complex Plane
Faisal Mohamed -
Motion of an n-Point Dynamical System
Faisal Mohamed -
Kaleidoscopic Polygons
Faisal Mohamed -
Exploring Cylindrical Coordinates
Faisal Mohamed -
Exploring Spherical Coordinates
Faisal Mohamed -
Kaiser Window Transform
Faisal Mohamed