Hill-Climbing Algorithm

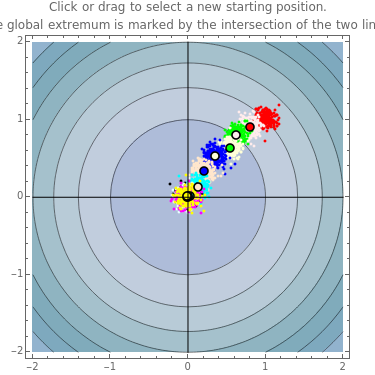
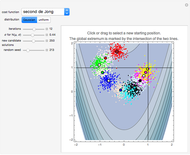
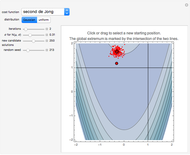
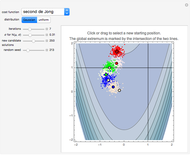
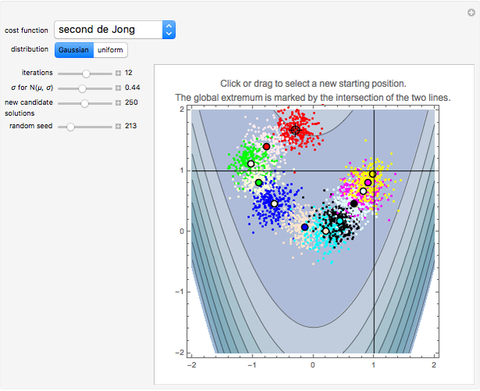
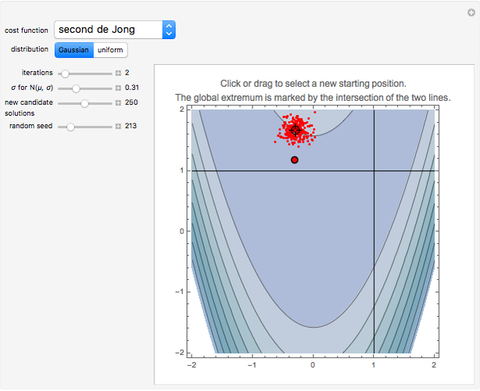
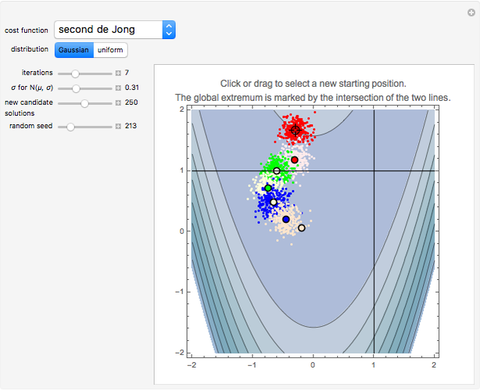
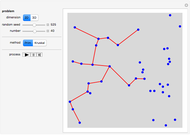
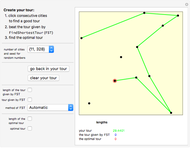
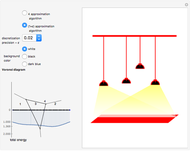
This simple version of hill-climbing algorithms belongs to the gradient methods, which search the space of possible solutions in the direction of the steepest gradient. Because it uses gradients, the algorithm frequently gets stuck in a local extreme. The basic version functions so that it always starts from the random point in the space of possible solutions. For the momentarily proposed solution, a certain neighborhood is determined using a final set of transformations and the given function is minimized only in this neighborhood. The local solution obtained is then used as a new starting point for the calculation of a new neighborhood. The solutions of each iteration are dots on the cost function landscape. The best solution for each iteration is marked by a thick dot with a black circle around it. Different colors represent different iterations in order: red, light pink, green, light yellow, blue, light orange, cyan, black, light cyan, magenta, yellow, light brown, orange, light purple, brown, light red, white, pink, purple, light green, and light blue.