Details

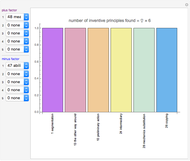
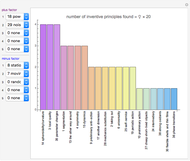
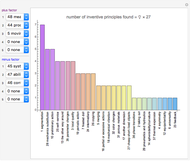
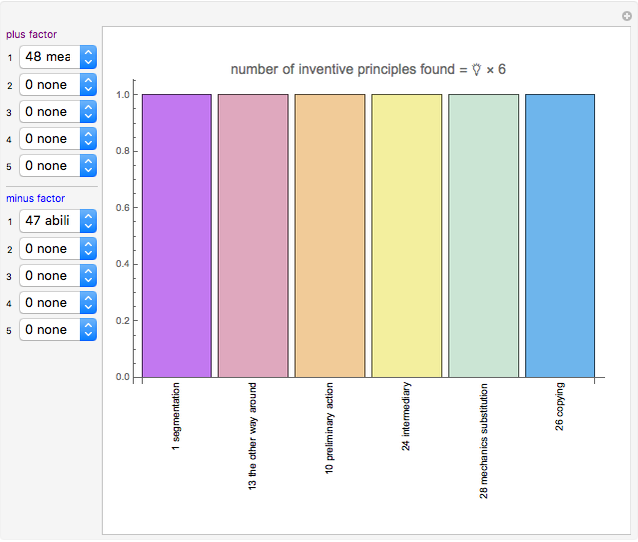
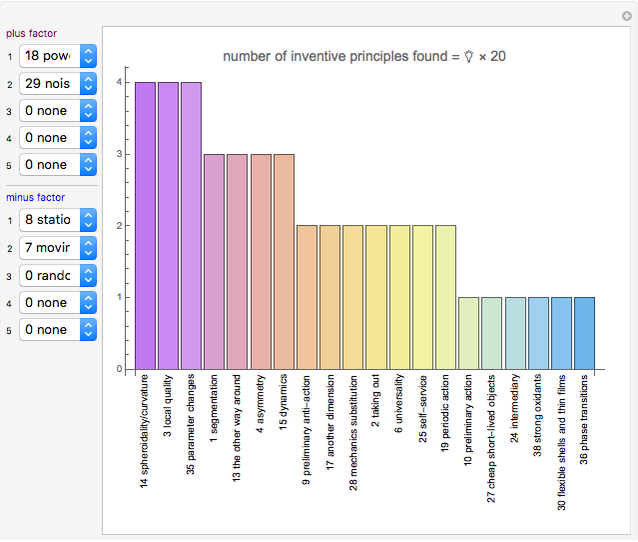
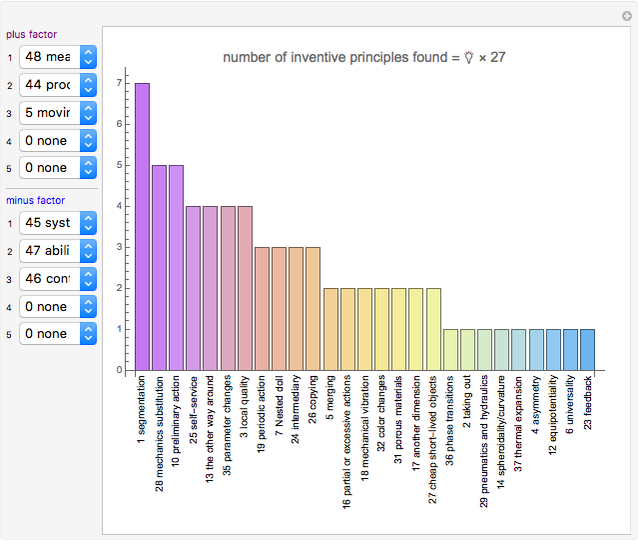
The source data is based on Mann's TRIZ matrix [3, 4]. This Demonstration uses the Mathematica function Tuples to generate all combinations between multiple advantage and disadvantage factors.

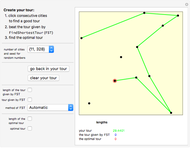
Snapshot 1: TRIZ matrix result with one advantage factor (1) against one disadvantage factor (1), as a case study for a precision measurement device

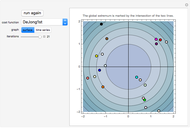
Snapshot 2: TRIZ matrix result with two advantage factors (2) against three disadvantage factors (3, including one random factor), as a case study for an advanced motor

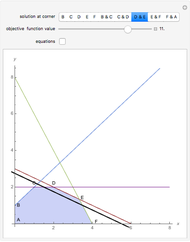
Snapshot 3: TRIZ matrix result with three advantage factors (3) against three disadvantage factors (3), as a case study for a wafer stage system or projection lithography in the microelectronic industry

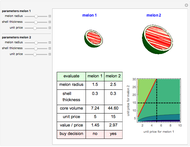
Snapshot 4: TRIZ matrix result with all advantage factors against all disadvantage factors, which exactly yields a frequency ranking of 40 inventive principles

References

[1] Wikipedia. "TRIZ." (Sep 5, 2016) en.wikipedia.org/wiki/TRIZ.

[2] G. Altshuller, The Innovation Algorithm: TRIZ, Systematic Innovation and Technical Creativity (L. Shulyak and S. Rodman, trans.), Worcester, MA: Technical Innovation Center, 1999.

[3] D. L. Mann, "Comparing the Classical and New Contradiction Matrix: Part 1—Zooming Out," The Triz Journal, 2004. triz-journal.com/comparing-classical-new-contradiction-matrix-part-1-zooming.

[4] D. L. Mann, "Comparing the Classical and New Contradiction Matrix: Part 2—Zooming In," The Triz Journal, 2004. triz-journal.com/comparing-classical-new-contradiction-matrix-part-2-zooming.

[5] L. Zheng, W. Fei and A. Bourov, "Learning TRIZ through Lithography-Electronics Co-evolution," in Proceedings of the 12th International MATRIZ Conference (TRIZfest-2016), Beijing, China (V. Souchkov, ed.), Knoxville, TN: International TRIZ Association, 2016 pp. 188–197. www.triz-event.com/TRIZfest2016Proceedings.pdf.

[6] G. Retseptor, "40 Inventive Principles in Microelectronics," The Triz Journal, 2002. triz-journal.com/40-inventive-principles-microelectronics.