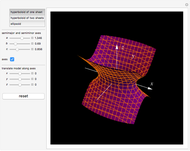
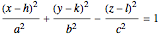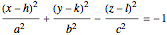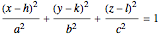Hyperboloids and Ellipsoids

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
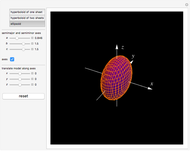
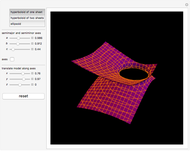
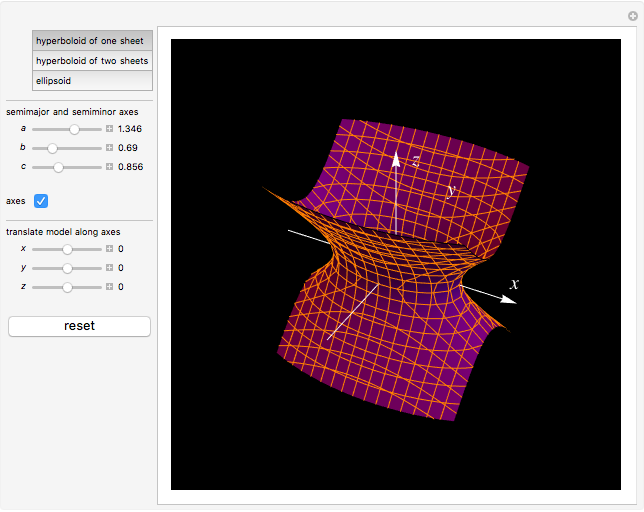
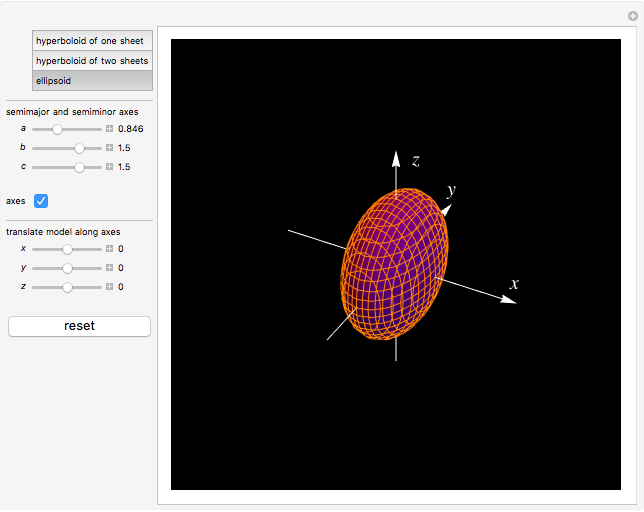
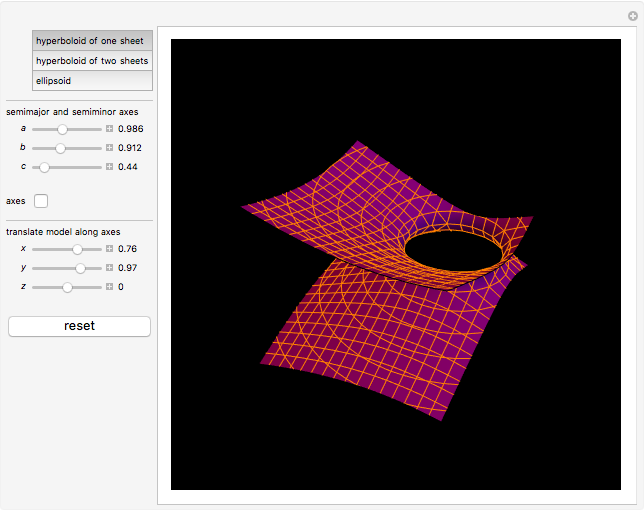
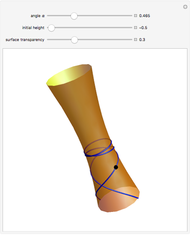
This Demonstration shows hyperboloids of one and two sheets as well as ellipsoids. When modeling ellipsoids, make the  ,
,  , and
, and  values equal to form a sphere.
values equal to form a sphere.
Contributed by: Lachlan Palmer (November 2014)
Open content licensed under CC BY-NC-SA
Snapshots
Details
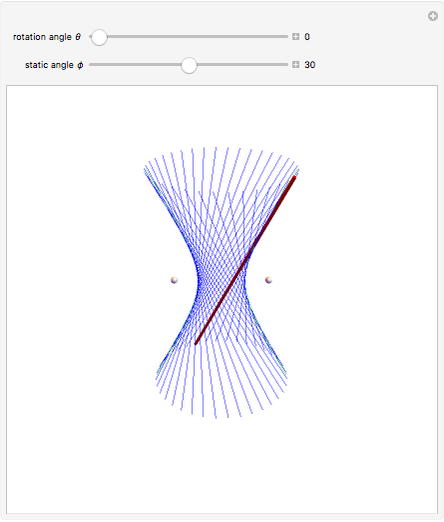
Hyperboloids are obtained by rotating a hyperbola.
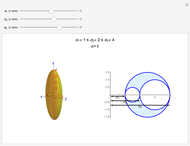
An ellipsoid is obtained when a 2D ellipse is rotated around either the semimajor or semiminor axis. However, the ellipsoid formed by rotating an ellipse on its semimajor axis will not be the same as the ellipsoid formed by rotating the ellipse on its semiminor axis. Also, there are ellipsoids that are not formed from the rotation of an ellipse; for example, 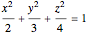 .
.
Permanent Citation