KAM Tori Reforming

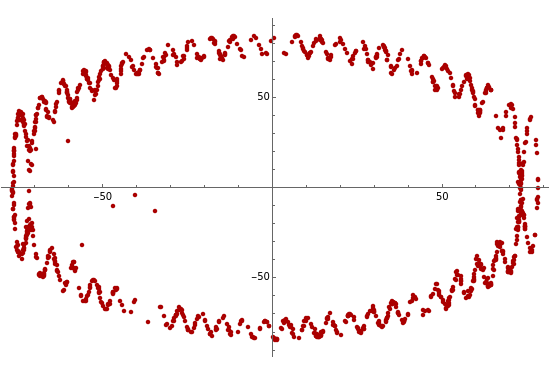
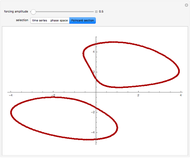
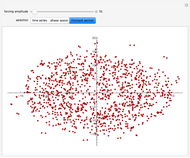
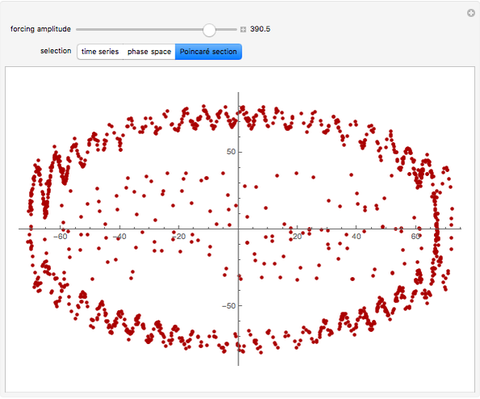
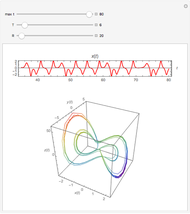
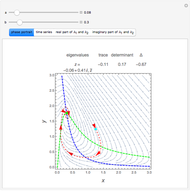
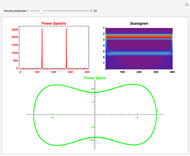
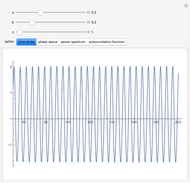
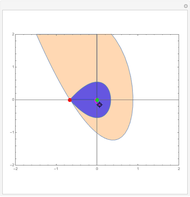
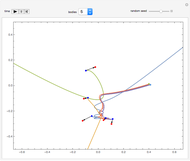
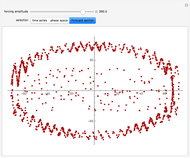
Under the influence of a small perturbation, the invariant manifolds of integrable Hamiltonian systems are slightly modified. The original manifolds are tori, according to the KAM theorem due to Kolmogorov, Arnold, and Moser. As the perturbation increases, the tori become progressively distorted and fully developed chaos sets in. But as the perturbation becomes increasingly large (infinite in the limit) chaos dissipates and tori form again, although they are not the same as those of the unperturbed system. Thus the conditions for the KAM theorem are recovered.