Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

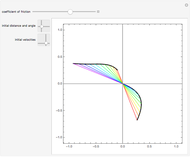
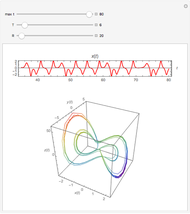
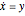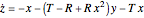Moore-Spiegel Attractor

Download to Desktop Copy to Clipboard
Source

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram CDF Player or other Wolfram Language products.

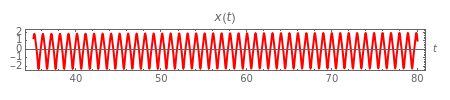
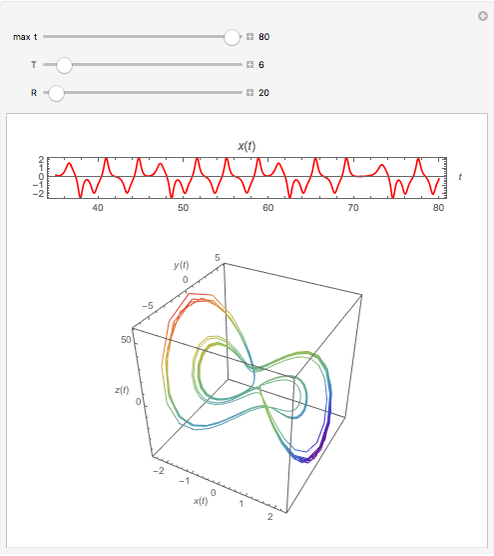
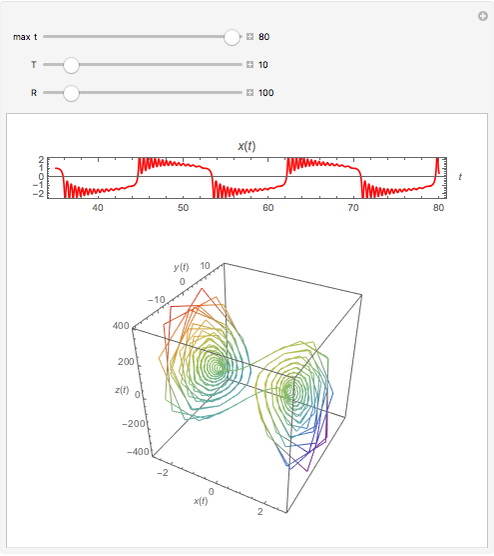
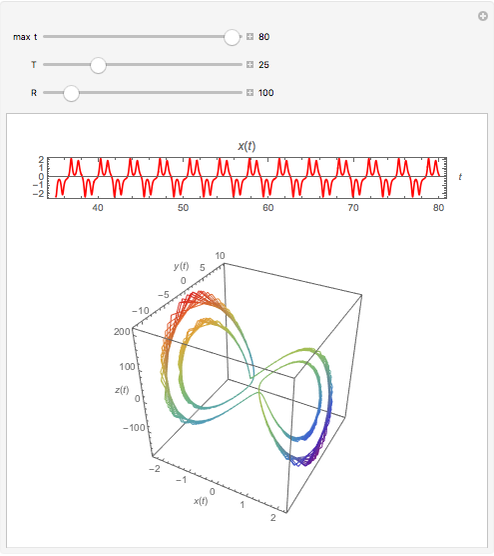
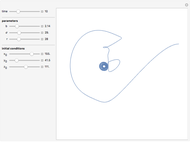
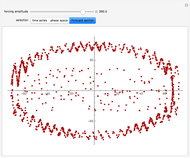
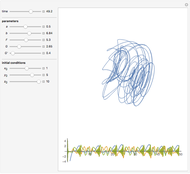
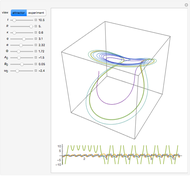
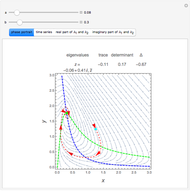
Requires a Wolfram Notebook System

Edit on desktop, mobile and cloud with any Wolfram Language product.

The Moore–Spiegel system is a nonlinear thermo-mechanical oscillator with displacement 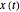. The parameter is analogous to the Prandtl number times the Rayleigh number, while 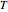is analogous to the Prandtl number times the Taylor number. The system describes a fluid element oscillating vertically in a temperature gradient with a linear restoring force.

[more]

The equations of the system are: , , .

Along with the Lorenz system, the Moore–Spiegel system is one of the classical low-order dynamical systems that exhibits chaos.

[less]

Contributed by: Milena Cuellar (May 2011)
After work by: E. A. Spiegel (1966)
Open content licensed under CC BY-NC-SA

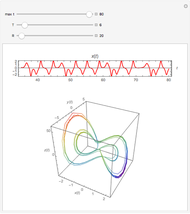
Snapshots

Details

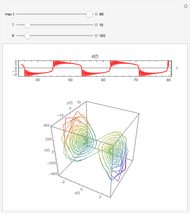
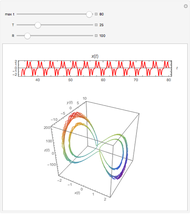
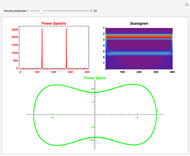
Snapshots 1, 3, 4, and 5: chaotic time series

Snapshots 2 and 6: periodic time series

References

[1] D. W. Moore and E. A. Spiegel, "A Thermally Excited Non-Linear Oscillator," Astrophysical Journal, 143, 1966 pp. 871–887.

[2] N. J. Balmforth and R. V. Craster, "Synchronizing Moore and Spiegel," Chaos, 7(4), 1997 pp. 738–752.

Embed Code

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send