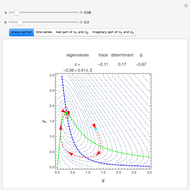
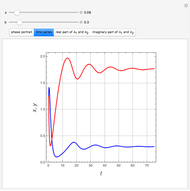
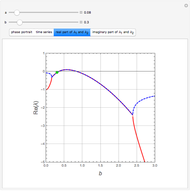
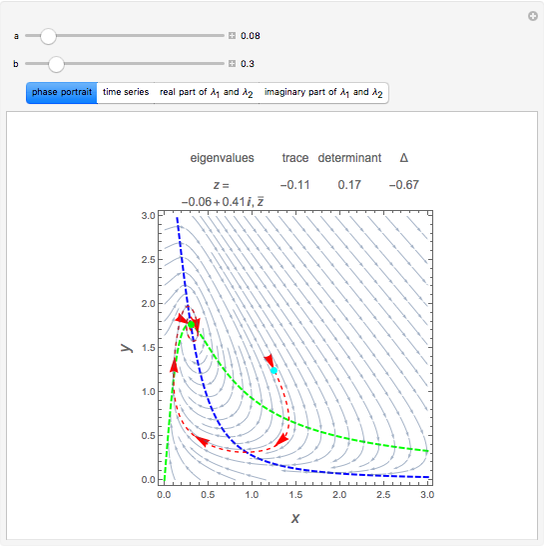
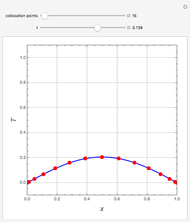
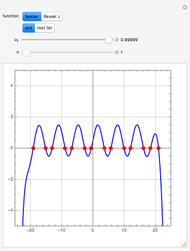
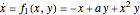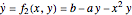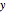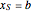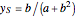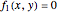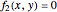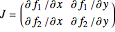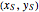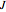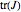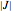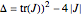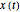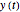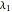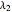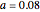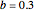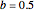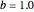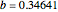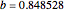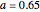In the study of nonlinear dynamics, it is useful to first introduce students to simple systems that exhibit periodic behavior as a consequence of a Hopf bifurcation. The two-dimensional nonlinear and autonomous system given by
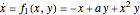 ,
,
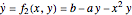
has this feature. These equations describe the autocatalytic reaction of two intermediate species  and
and 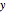 in an isothermal batch reactor, when the system is far from equilibrium [1]. In this context, the steady state referred to below is a pseudo steady state, and is applicable when the precursor reactant is slowly varying with time.
in an isothermal batch reactor, when the system is far from equilibrium [1]. In this context, the steady state referred to below is a pseudo steady state, and is applicable when the precursor reactant is slowly varying with time.
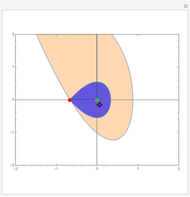
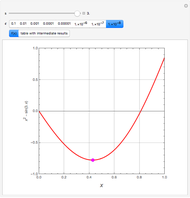
The unique steady state is given by 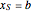 and
and 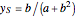 . This steady state is at the position of the green dot in the phase portrait diagram. It appears as the intersection of the dotted blue and green curves, which are the level curves given by
. This steady state is at the position of the green dot in the phase portrait diagram. It appears as the intersection of the dotted blue and green curves, which are the level curves given by 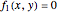 and
and 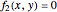 .
.
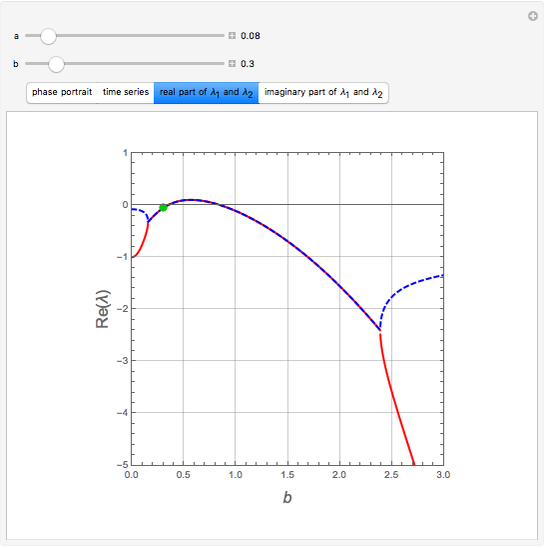
The stability of steady state to small disturbances can be assessed by determining the eigenvalues of the Jacobian 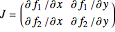 . A Hopf bifurcation occurs when a complex conjugate pair of eigenvalues crosses the imaginary axis.
. A Hopf bifurcation occurs when a complex conjugate pair of eigenvalues crosses the imaginary axis.
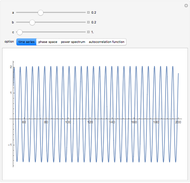
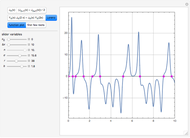
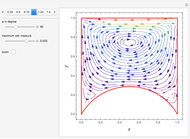
This Demonstration shows the phase portrait with the vector field of directions around the critical point 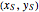 . In addition, the eigenvalues of
. In addition, the eigenvalues of 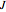 , the trace
, the trace 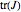 , the determinant
, the determinant 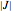 , and
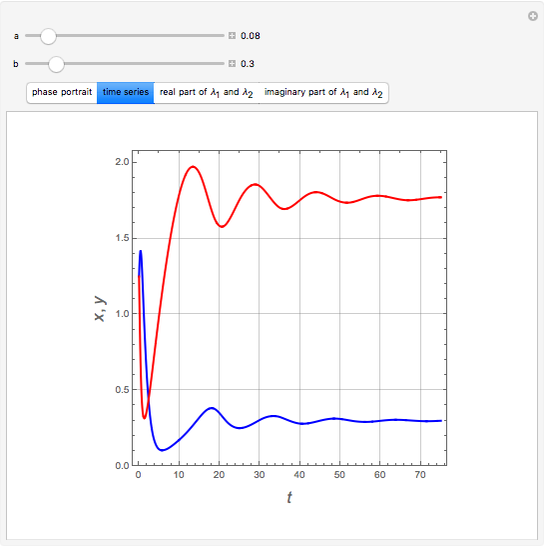
, and 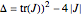 are computed. The time series are also plotted in a separate diagram (the blue and red curves correspond to
are computed. The time series are also plotted in a separate diagram (the blue and red curves correspond to 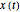 and
and 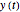 , respectively. Finally, the real and imaginary parts of the two eigenvalues
, respectively. Finally, the real and imaginary parts of the two eigenvalues 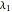 and
and 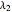 are plotted (in blue and red, respectively) versus
are plotted (in blue and red, respectively) versus  for user-specified values of the parameter
for user-specified values of the parameter  .
.
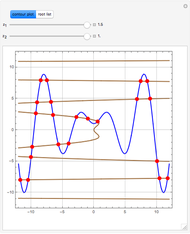
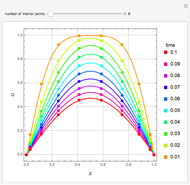
To observe a Hopf bifurcation, you can set 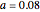 and vary
and vary  . As you can see in the snapshots, there are two Hopf bifurcation points. Indeed, for
. As you can see in the snapshots, there are two Hopf bifurcation points. Indeed, for 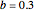 , the steady state is a stable focus; for
, the steady state is a stable focus; for 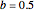 , the trajectory is attracted to a stable periodic solution (called a limit cycle); and finally for
, the trajectory is attracted to a stable periodic solution (called a limit cycle); and finally for 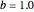 , the steady state is again a stable focus. For
, the steady state is again a stable focus. For 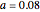 , the two Hopf bifurcation points are obtained at
, the two Hopf bifurcation points are obtained at 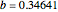 and
and 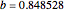 . Finally, the last snapshot (obtained for larger values of
. Finally, the last snapshot (obtained for larger values of  , for instance,
, for instance, 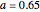 ), the Hopf bifurcation disappears and there are only transitions from a stable node to a stable focus and then back to stable node.
), the Hopf bifurcation disappears and there are only transitions from a stable node to a stable focus and then back to stable node.
[less]