Least-Squares Estimation of an Ellipse
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
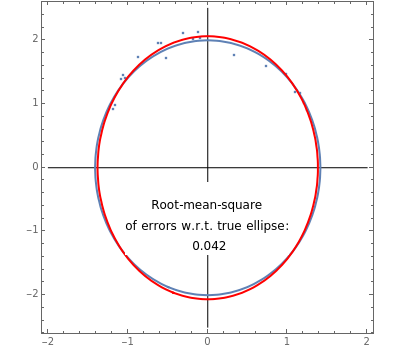
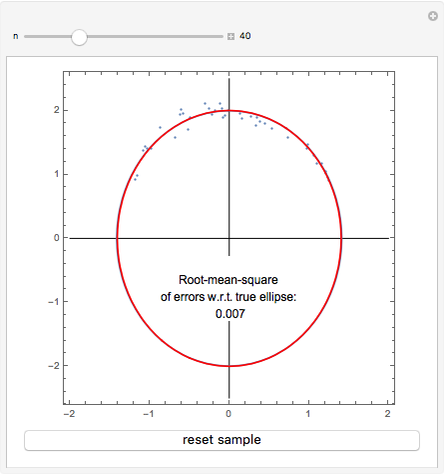
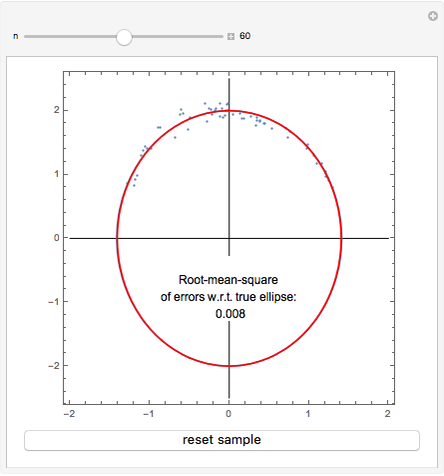
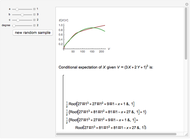
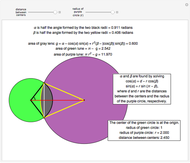
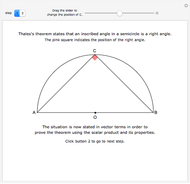
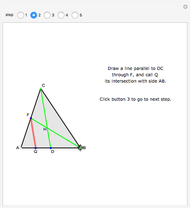
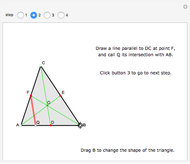
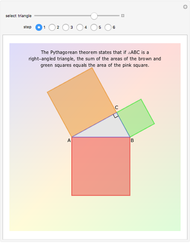
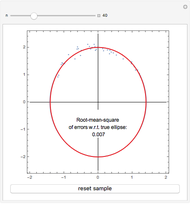
Given the ellipse 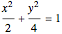 , a random sample of uniformly distributed abscissae in the interval
, a random sample of uniformly distributed abscissae in the interval  is generated. From these a set of ordinates is obtained by adding to each corresponding point on the ellipse a normally distributed error with mean 0 and standard deviation 0.1. The set of points thus obtained is used to estimate the parameters of the ellipse with the least-squares method.
is generated. From these a set of ordinates is obtained by adding to each corresponding point on the ellipse a normally distributed error with mean 0 and standard deviation 0.1. The set of points thus obtained is used to estimate the parameters of the ellipse with the least-squares method.
Contributed by: Tomas Garza (March 2011)
Open content licensed under CC BY-NC-SA
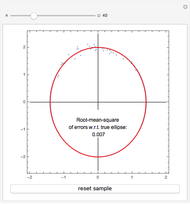
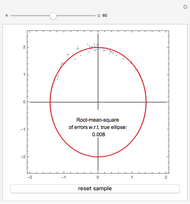
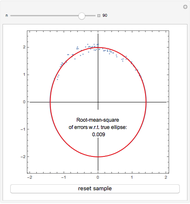
Snapshots
Details
Permanent Citation