Linear State Estimation Using a Weighted Least-Squares Method

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
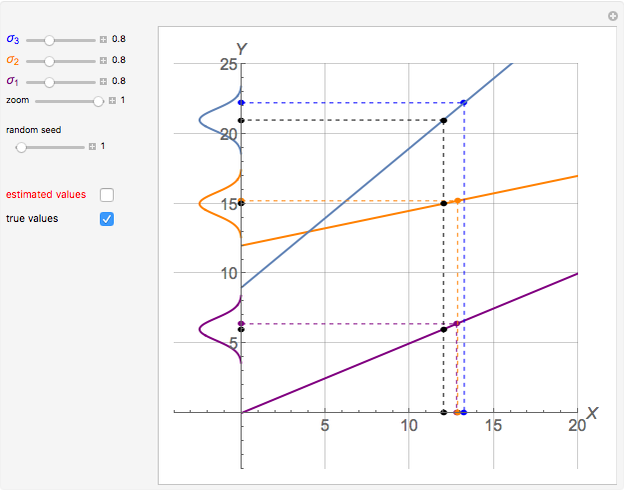
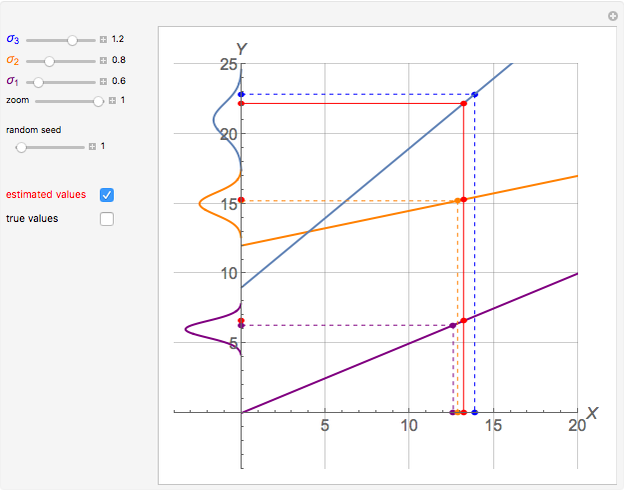
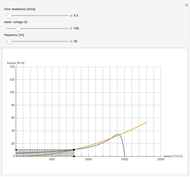
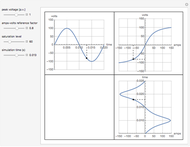
Vary the variances of three measurements performed on a linear system to observe the changes in the estimation of the single state variable. The state variable is estimated using a weighted least-squares method. The system is linear simply because linear functions describe the variation of the measured quantities with changes in the state variable. Optionally, you can see the true values of the state variable and the measured quantities, as well as the state variable estimate and the recalculated values for the three measurements. You can zoom to see details on the 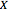 axis.
axis.
Contributed by: Diego M. Ferreyra (February 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
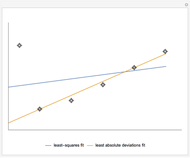
State estimation consists of using a statistical criterion to assign values to a set of (unknown) state variables, based on a set of measurements performed on the system. Since most state variables are unknown in a real-life system, they have to be estimated from the measurements that can actually be performed. The values assigned to the state variables by means of a state estimation technique are called state variable estimates. State estimation can be performed on either linear or nonlinear systems.
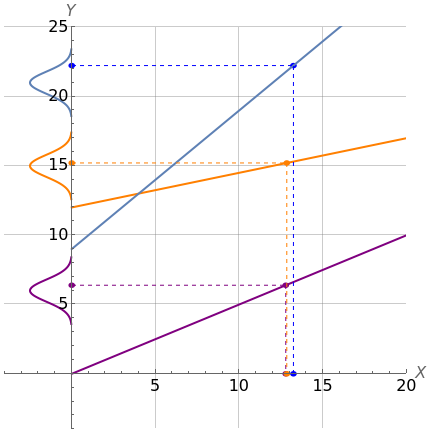
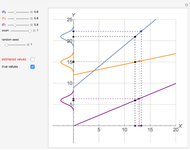
This Demonstration represents a linear system with a single state variable (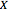 axis) and three different quantities (
axis) and three different quantities (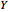 axis) that are measured. Assume that the system's model is known in full; then the graph shows the linear relationships describing the values of each of the three measured quantities as functions of the state variable.
axis) that are measured. Assume that the system's model is known in full; then the graph shows the linear relationships describing the values of each of the three measured quantities as functions of the state variable.
The measurements include normal distribution errors, which describe the usual fact that measuring a given quantity never yields its true value but a value resulting from adding a zero-mean Gaussian error to the true value.
From these deliberately inaccurate measurements, an estimate for the state variable is calculated using a weighted least-squares method. To this effect, variance-based measurement weight factors are applied. Namely, small-variance measurements, obtained from the best measuring instruments, are preponderant when it comes to calculating the estimate; on the other hand, measurements with larger variances (coming from worse instruments) have smaller weighting factors and a lower impact on the determination of the state variable estimate.
Permanent Citation