Confidence Intervals for the Binomial Distribution

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
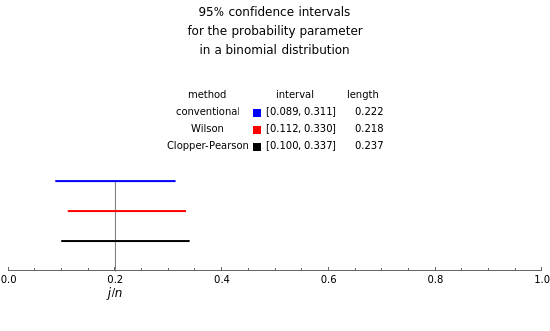
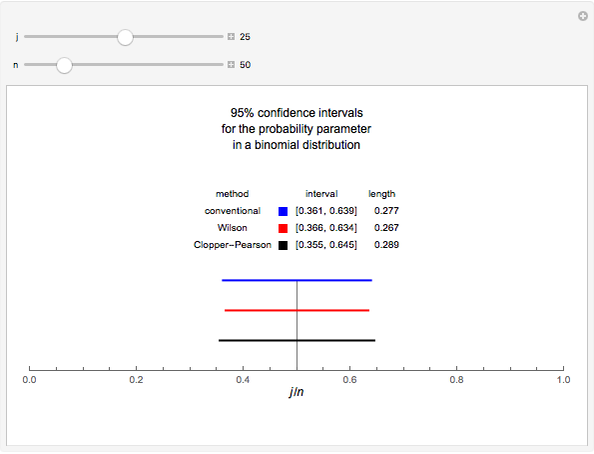
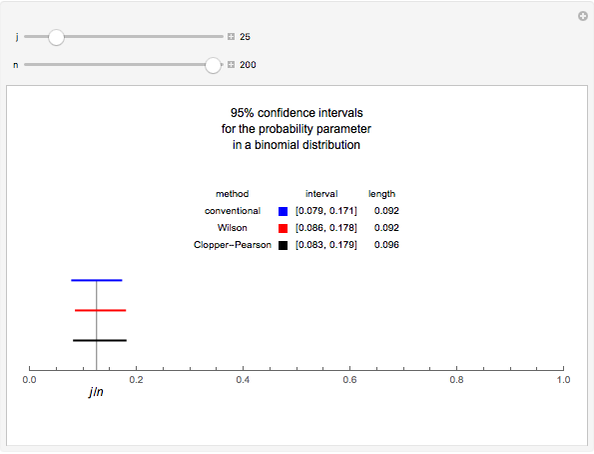
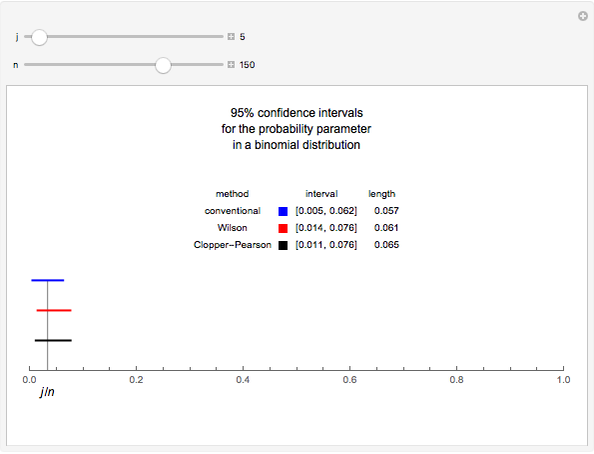
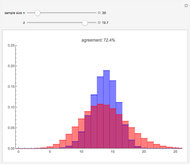
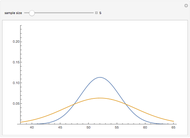
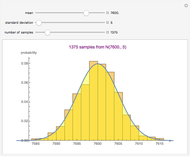
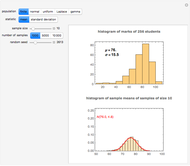
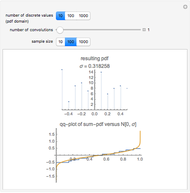
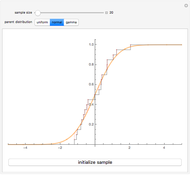
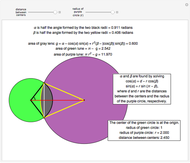
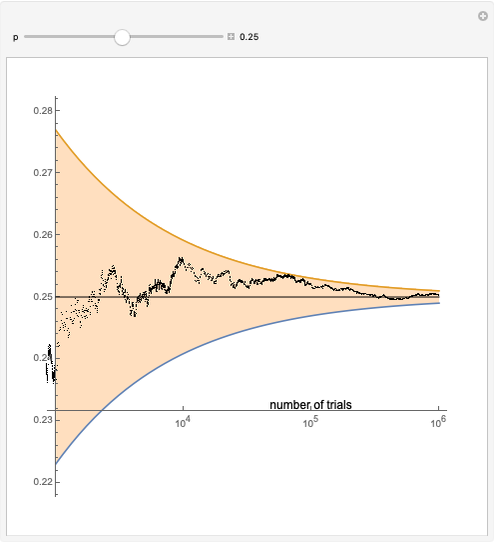
A confidence interval for estimating a parameter of a probability distribution must show two basic properties. First, it must contain the value of the parameter with a prescribed probability, and second, it must be as short as possible in order to be useful. Confidence intervals may be derived in different ways. In the case of a binomial distribution with  trials and probability parameter
trials and probability parameter 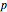 , the conventional method for estimating
, the conventional method for estimating 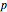 uses the normal approximation and produces an interval centered at the point
uses the normal approximation and produces an interval centered at the point  , where
, where 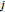 is the number of successes obtained in the
is the number of successes obtained in the  trials.
trials.
Contributed by: Tomas Garza (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
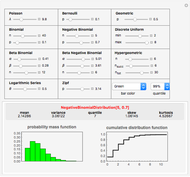
The article on Binomial proportion confidence interval in Wikipedia gives the details for Wilson's method. Implementation of the Clopper–Pearson method is due to the author of this presentation.
Permanent Citation