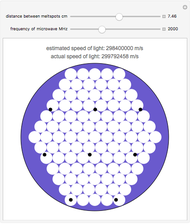
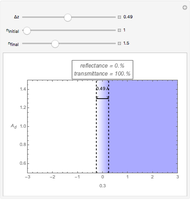
Light Propagation at Soft Interface

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
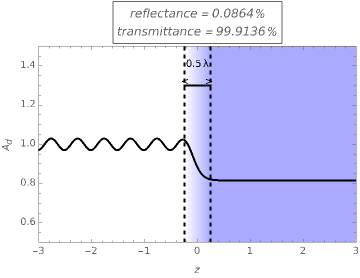
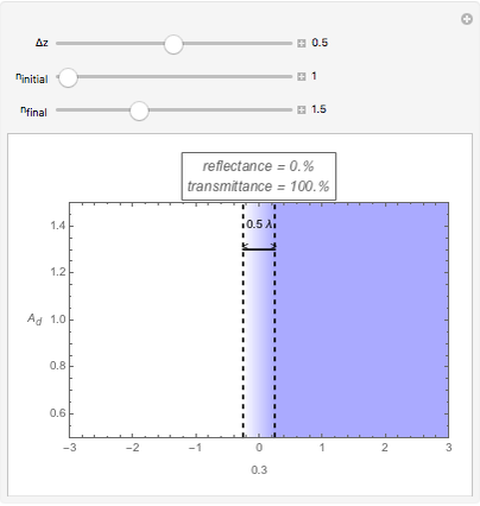
This Demonstration shows how light is reflected when it propagates through a "soft", transparent interface where the refractive index varies continuously. You can vary this thickness, 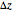 . The blue area represents the medium's refractive index, from completely transparent in a vacuum to dark blue for
. The blue area represents the medium's refractive index, from completely transparent in a vacuum to dark blue for 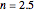 . You can also vary the initial and final refractive indices
. You can also vary the initial and final refractive indices 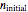 and
and 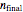 . Light propagation is always normal to the interface; incident light comes from the left and propagates toward the right.
. Light propagation is always normal to the interface; incident light comes from the left and propagates toward the right.
Contributed by: Noe Atzin, Manuel Fernandez-Guasti, and Ruth Diamant (December 2010)
Open content licensed under CC BY-NC-SA
Snapshots
Details
We know very well how light is reflected on an abrupt surface, for example, how light is reflected on a perfect glass surface. But when the refractive index varies continuously, the problem is not so simple. Maxwell's equations are solved here with no approximations regarding the interface abruptness or softness. Provided that an exact invariant exists, this leads to the Ermakov equation for the electric field amplitude.
This Demonstration shows how light is reflected when it propagates through such a "soft" interface, where the refractive index varies continuously along a certain distance 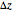 . You can vary this thickness, which is measured in wavelength units. The refractive index profile varies as a hyperbolic tangent function. The program can be easily modified to allow for different profiles.
. You can vary this thickness, which is measured in wavelength units. The refractive index profile varies as a hyperbolic tangent function. The program can be easily modified to allow for different profiles.
The Demonstration shows the relative amplitude of the light wave’s electric field as a function of position. This amplitude can be separated as a superposition of the incident and reflected waves far from the interface. When there are counter propagating waves, the amplitude exhibits oscillations. The intensity reflectance and transmittance shown above the graph are evaluated from the maxima and minima of the amplitude oscillations. In the very soft limit, called the adiabatic limit, the reflection becomes negligible. In the abrupt limit, the reflectivity becomes identical to Fresnel's analytic coefficients. The invariant procedure and the solutions for different refractive index profiles are described in [1] and [2].
The notation used is:
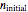 = initial refractive index of the incident wave medium far from the interface
= initial refractive index of the incident wave medium far from the interface
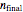 = final refractive index of the incident wave medium far from the interface
= final refractive index of the incident wave medium far from the interface
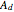 = dimensionless total wave amplitude as a function of position
= dimensionless total wave amplitude as a function of position
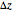 = distance where the refractive index varies 90% in wavelength units (
= distance where the refractive index varies 90% in wavelength units (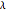 )
reflectance = quotient of reflected intensity over incident intensity
trans = quotient of incident amplitude over reflected amplitude
transmittance = quotient of transmitted irradiance over incident irradiance
)
reflectance = quotient of reflected intensity over incident intensity
trans = quotient of incident amplitude over reflected amplitude
transmittance = quotient of transmitted irradiance over incident irradiance
 = a measure of the refractive index variation, equal to
= a measure of the refractive index variation, equal to 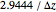
References
[1] M. Fernández–Guasti, A. G. Villegas, and R. Diamant, "Ermakov Equation Arising from Electromagnetic Fields Propagating in 1D Inhomogeneous Media," Revista Mexicana de Física, 46(6), 2000, pp. 530–538. Ermakovequation.pdf.
R. Diamant and M. Fernández-Guasti, "Light Propagation in 1D Inhomogeneous Deterministic Media: The Effect of Discontinuities," Journal of Optics A: Pure and Applied Optics, 11(4), 2009, p. 045712. http://stacks.iop.org/1464-4258/11/045712.
Permanent Citation