Propagation of Reflected and Refracted Waves at an Interface

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
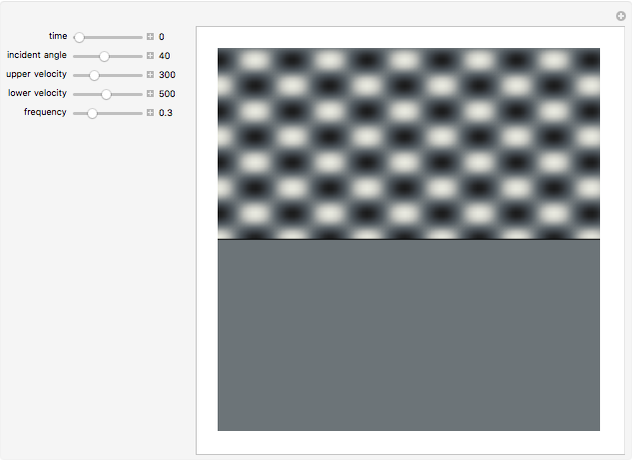
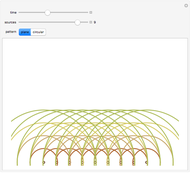
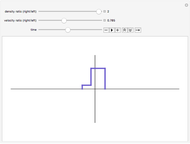
A propagating wave of given frequency (in Hz) is incident on an interface between two acoustic media, with varying propagation velocities. The incident angle is measured from the vertical, running from 0 to 90 degrees. The amplitudes of the reflected and refracted waves are computed for the specified incident angle. The reflected wave is added to the incident wave in the upper medium and the refracted wave is shown in the lower medium. At a certain incident angle that depends on the relative velocities, the incident wave will be totally reflected and the bottom half of the plot will become solid gray, indicating zero amplitude.
Contributed by: David von Seggern (University of Nevada) (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
This Demonstration shows how a propagating plane wave interacts with an interface between two acoustic media. The incident wave impinges on the boundary from the top and causes a reflected wave that interferes with the incident wave. The incident wave is transmitted into the bottom layer as a refracted wave with its own propagation velocity. The incident and refracted wave angles  (angle of the wave normal relative to vertical) are related by the well-known equation
(angle of the wave normal relative to vertical) are related by the well-known equation
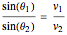 ,
,
where  is velocity and the subscripts 1 and 2 denote the top and bottom media. The incident wave is taken to have amplitude 1. If
is velocity and the subscripts 1 and 2 denote the top and bottom media. The incident wave is taken to have amplitude 1. If 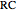 denotes the reflection coefficient for the scattered wave amplitudes, then the wave motion in the top layer is described by (Towne, 1988)
denotes the reflection coefficient for the scattered wave amplitudes, then the wave motion in the top layer is described by (Towne, 1988)
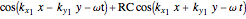 ,
,
while, with 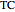 denoting the transmission coefficient, the motion in the bottom layer is described by
denoting the transmission coefficient, the motion in the bottom layer is described by
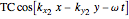 ,
,
where 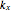 and
and  are the horizontal and vertical wavenumbers, with the subscripts 1 and 2 for the top and bottom layers, respectively, and
are the horizontal and vertical wavenumbers, with the subscripts 1 and 2 for the top and bottom layers, respectively, and  is the frequency in radians. Here all lengths are in meters.
is the frequency in radians. Here all lengths are in meters.
The coefficients 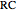 and
and 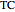 are computed for variable angles of incidence and velocities with
are computed for variable angles of incidence and velocities with
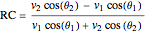 ,
,
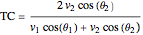 ,
,
assuming, with no loss of generality, that the densities of the two media are equal. This definition puts 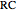 in the range
in the range 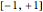 , while
, while 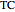 has the range
has the range 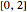 . Because of wave interference, the top media can have amplitudes in the range
. Because of wave interference, the top media can have amplitudes in the range 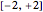 . The overall amplitudes are scaled in the plots such that black is -2, white is +2, and medium gray is 0. Note that amplitudes appear to be continuous across the boundary. This physical fact is the basis for the equations for computation of
. The overall amplitudes are scaled in the plots such that black is -2, white is +2, and medium gray is 0. Note that amplitudes appear to be continuous across the boundary. This physical fact is the basis for the equations for computation of 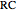 and
and 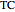 .
.
Reference:
D. H. Towne, Wave Phenomena, New York: Dover Publications, 1988.
Permanent Citation