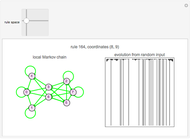
Local Markov Chains for Elementary Cellular Automata

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
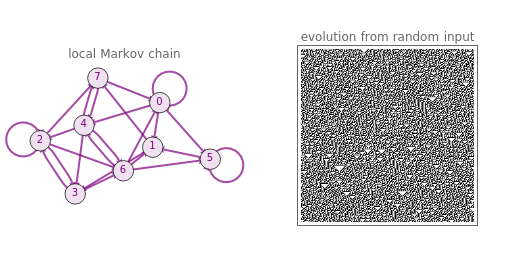
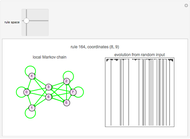
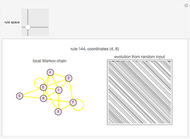
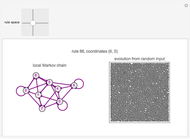
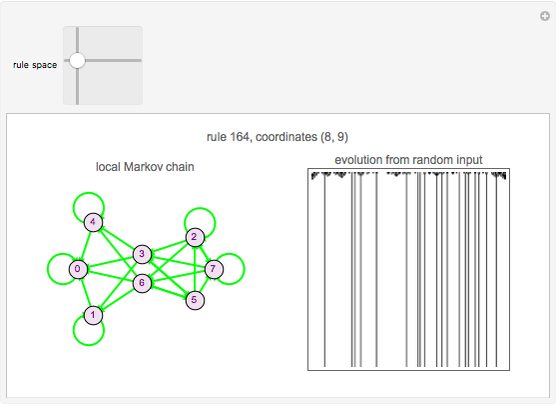
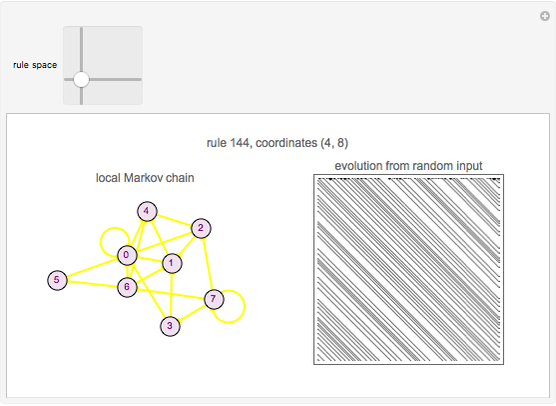
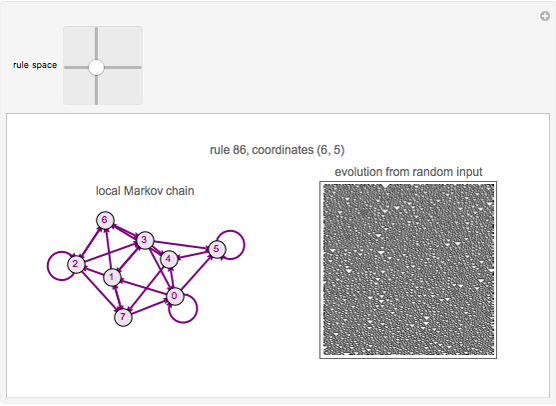
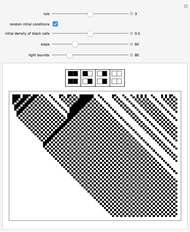
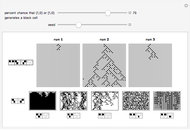
Cellular automata (CA) are defined by a mapping from the values of a cell and its neighbors to the next value of that cell. If the value of a cell and its neighborhood are matched to a state, the next state of that range can be defined if the values of the cells to the right and left of the range are also known. Assume that the values in the cells immediately to the right and left of the neighborhood are equally likely. With this information, create a local Markov chain (LMC) for a given range of a cell and its neighborhood. This Demonstration shows the LMC for the elementary cellular automata; you select the rule from the 2D slider that represents the rule space. The coordinates represent the primitives that make up the rule, according to the author's previous research. The colors of the edges correspond to the Wolfram class: green for class 1, yellow for class 2, purple for class 3, and red for class 4.
Contributed by: Rodrigo A. Obando (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Snapshot 1: class 1 cellular automaton
Snapshot 2: class 2 cellular automaton
Snapshot 3: class 3 cellular automaton
Snapshot 4: class 4 cellular automaton
More information about the author (NKS|Online) and his work is available.
Permanent Citation
"Local Markov Chains for Elementary Cellular Automata"
http://demonstrations.wolfram.com/LocalMarkovChainsForElementaryCellularAutomata/
Wolfram Demonstrations Project
Published: March 7 2011