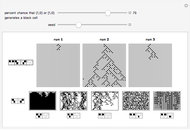
Prospecting for Complexity in k=3, r=1 Cellular Automata

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
Exploring the 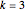 ,
,  one-dimensional cellular automata (CA) with over 7 trillion rules is daunting. This rule explorer attempts to collect rules with similar behavior together, and furthermore, to create a feeling of control when prospecting for simple or complex behavior.
one-dimensional cellular automata (CA) with over 7 trillion rules is daunting. This rule explorer attempts to collect rules with similar behavior together, and furthermore, to create a feeling of control when prospecting for simple or complex behavior.
Contributed by: John Kiehl (March 2011)
Based on a program by: Stephen Wolfram
Open content licensed under CC BY-NC-SA
Snapshots
Details
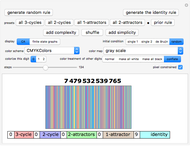
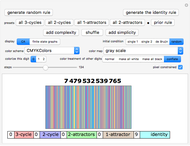
Snapshot 1: the simple, vertical stripes characteristic of the identity rule 7,479,532,539,765 in 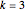 ,
,  CA
CA
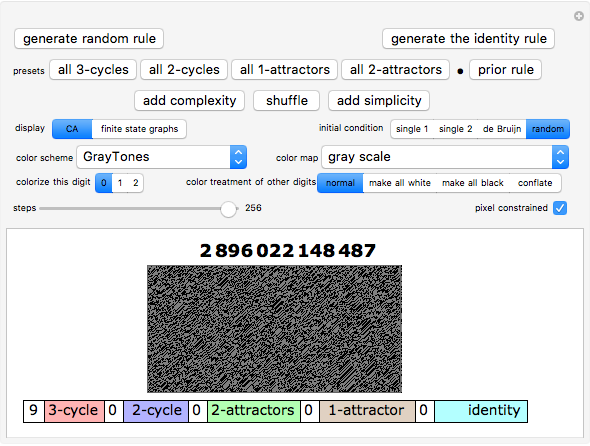
Snapshot 2: rules composed solely of 3-cycle patterns typically create chaotic, complex global behavior
Snapshot 3: but here is an all 3-cycle rule with class 2 behavior—perfect for wallpaper designs (!)
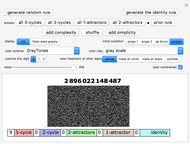
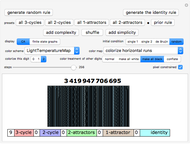
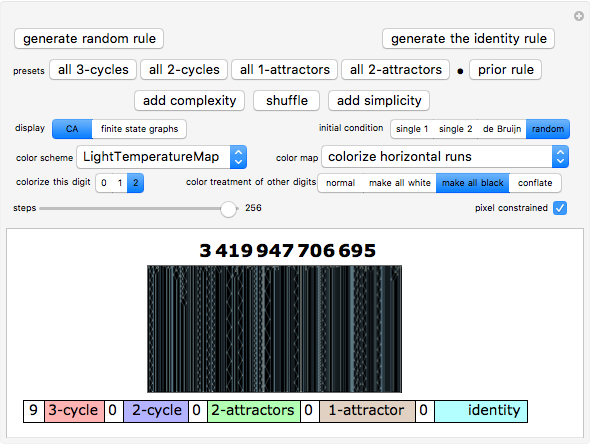
Snapshots 4, 5, 6: various color schemes bring out various details of these all 2-cycle patterns
Snapshots 7, 8, 9: three different initial conditions of the same rule create three different patterns; typically the de Bruijn sequence of digits most resembles the behavior of a completely random initial condition
Snapshot 10: normally you focus on the behavior of one digit, colorizing only one of the three digits 0, 1, or 2
Snapshot 11: setting the other two, unfocused digits to black (or white) emphasizes the patterns of the focused digit
Snapshot 12: the "conflate" option preserves the "normal" option's shades of gray but maps them to two shades from the chosen color scheme
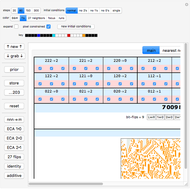
Snapshot 13: shows the underlying finite state machine configurations of a randomly generated rule
Snapshot 14: shows the underlying finite state machine configurations after clicking the "all 2-cycles" preset button, in which there is always a cyclic path between two of the vertices
Snapshot 15: shows the underlying finite state machine configurations of the identity rule, in which there is no transitioning from state to state
The Finite State Machine Model
In a 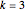 ,
,  CA rule, there are three input conditions that have the same left and right neighbors. For example, the center bits of these three input codes: {2,2,1}, {2,1,1}, {2,0,1} all have 2 as a left neighbor and 1 as a right neighbor. There are nine such possible neighborhood configurations, and these are exactly the nine plots shown in the finite state display of this Demonstration.
CA rule, there are three input conditions that have the same left and right neighbors. For example, the center bits of these three input codes: {2,2,1}, {2,1,1}, {2,0,1} all have 2 as a left neighbor and 1 as a right neighbor. There are nine such possible neighborhood configurations, and these are exactly the nine plots shown in the finite state display of this Demonstration.
Now, let us pretend that these two neighbor cells never change while the center cell travels on its orbit determined by the rule. So, for example, continuing with our three input codes above, if the center cells of these three input codes transition to {1}, {2}, {0} respectively, we could represent this neighborhood as a finite state machine: (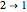 ,
, 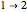 ,
, 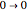 ), which is a 2-cycle with a single attractor. Even in face of the fallacy of such a model—since of course the neighbors do not remain constant—could we expect that rules rich in cyclical orbits tend to be complex while rules rich in stationary orbits tend to be simple? Could we expect to find that rules with the same population of finite state machine configurations have the same complexity? Is it possible that this model is as reasonable a way as any to explore slight perturbations from a given configuration?
), which is a 2-cycle with a single attractor. Even in face of the fallacy of such a model—since of course the neighbors do not remain constant—could we expect that rules rich in cyclical orbits tend to be complex while rules rich in stationary orbits tend to be simple? Could we expect to find that rules with the same population of finite state machine configurations have the same complexity? Is it possible that this model is as reasonable a way as any to explore slight perturbations from a given configuration?
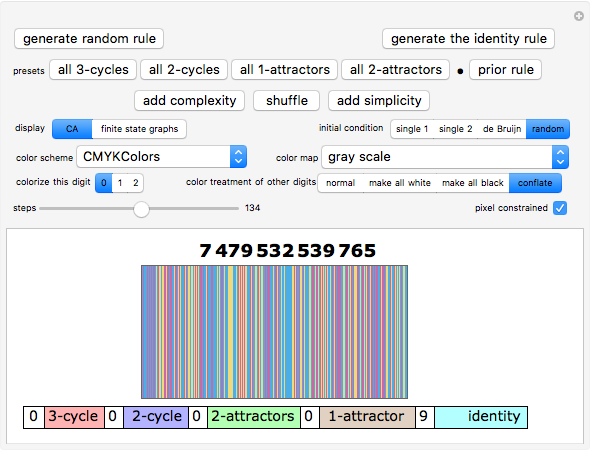
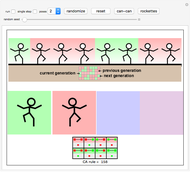
The finite state machine configurations fall naturally into five categories. A hierarchy of the five categories was created which leads from simple to complex behavior: the identity configuration (no movement); the single attractor, where all three digits 0, 1, and 2 are attracted to one of these digits; the double attractor, where one of the initial digits is absorbed into one of the other two digits; the 2-cycle, where the major characteristic is the oscillation of two of the initial digits and the third digit either is absorbed into the cycle or remains stationary; and the 3-cycle, which in traditional cycle notation would be notated either as (210) or (012).
The "add complexity" and "add simplicity" buttons change one neighborhood's finite state machine according to this hierarchy. The "shuffle" button does not change any of the finite state machine configurations, but rather shuffles them around to different neighborhoods.
Within each of the five categories there are many configurations. There are (the colors indicate the background): 2 types of 3-cycles (red) 9 types of 2-cycles (blue) 9 types of 1-attractors (brown) 6 types of 2-attractors (green) 1 identity or 3-attractor (cyan) If you click the preset buttons while watching the finite state graphs you will get a feeling for these choices. Clicking a preset button repeatedly will randomly choose from the allowed configurations, allowing for great variation.
Across the bottom of the display is the current census of configurations present in the current rule. This means clicking the "shuffle" button would not change any of these values, but clicking either the "add complexity" or "add simplicity" button would.
Miscellaneous Controls
"initial condition": As Snapshots 7, 8, and 9 show, using a single 1 digit or a single 2 digit can be very misleading about the overall behavior of a rule. The de Bruijn option provides a sequence of digits that are the smallest run of the three digits 0, 1, 2 which, when parsed in groups of three, include all 27 possible arrangements of the three base-3 digits. For more information see "De Bruijn Sequences Provide Compact Initial Conditions" (Wolfram Demonstrations Project).
"prior rule": Oftentimes while exploring you will zoom past an interesting rule. This button is provided to backtrack to the most recent rule.
"steps" slider and "pixel constrained" toggler: Setting the pixel constrained option to true creates a sharper picture. However, this comes at the expense of a stable picture when you adjust the "steps" slider. The author usually sets the number of steps to 124 and turns the pixel constrained option on.
Suggested Experiments
1. Click the "identity rule" button. Choose your favorite initial condition; the author prefers using the de Bruijn sequence for this strategy. Click the "add complexity" button until some class 3 or class 4 behavior shows up. This can take as many as 15 to 22 clicks. Click the "shuffle" button repeatedly, and get a sense of how robust the complex behavior is.
2. Click the "identity rule" button. This time after every "add complexity" click, click the "shuffle" button about 10 times to see if complex behavior shows up. The best the author has done was to discover complexity after just six "add complexity" clicks.
3. Click the "all 3-cycles" button. You will probably get a complex pattern, so transition to simple behavior. Alternate between clicking the "add simplicity" and the "shuffle" button. Strangely enough, a high percentage of these "energetic" rules are only class 2.
4. Click the "all 2-cycles" button. Click the "shuffle" button repeatedly. You should notice a similar balance between class 1-2 and class 3-4 behavior as in experiment 3. With an obvious class 3-4 pattern, click "add simplicity" repeatedly and measure how robust this configuration is for complexity.
5. Click the "generate random rule" button. You will get a complex pattern about two-thirds of the time. Click the "add simplicity" button until the complex behavior goes away. Now click "shuffle" until the complex behavior returns. Repeat the last two steps until you feel like you will never see complex behavior again. How many identity finite state machines do you have at this point?
A reasonable goal for the user would be to develop a sense of the impossibility of predicting or finding complex or simple behavior from a set of parameters.
Permanent Citation