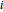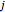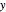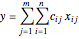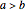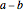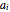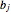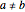Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Monge-Kantorovich Transportation Problem

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

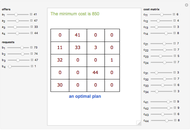
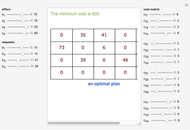
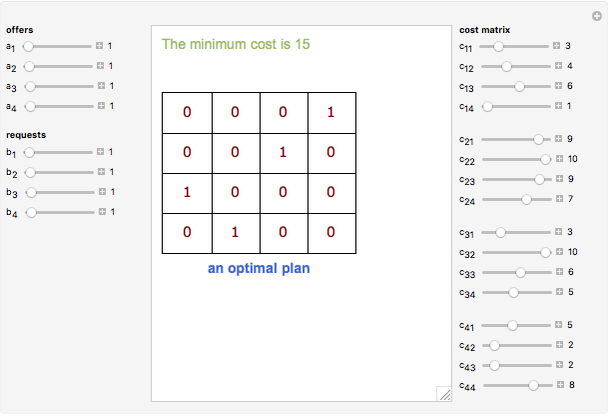
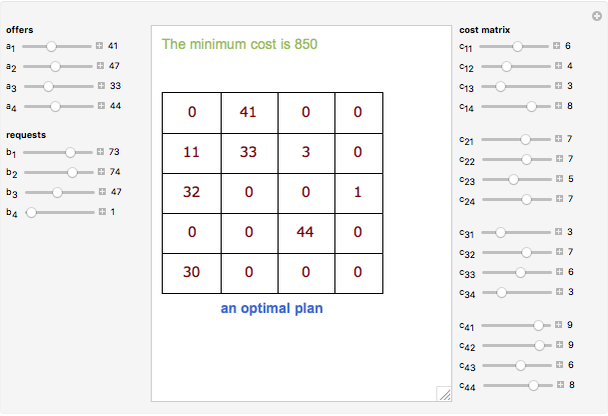
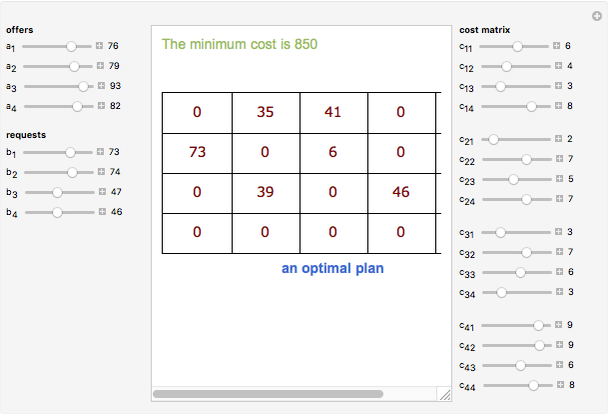
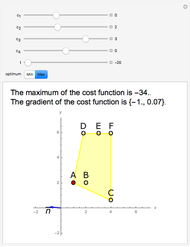
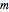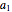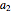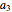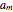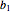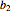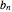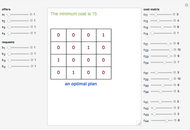
Some homogeneous goods are stocked in storage centers in quantities , , , …, . The goods are required in corresponding consumption centers , , , …, . Knowing the unit transportation costs 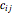from each storage center to each consumption center, a plan that uses all the goods (offers) and satisfies all the consumers (requests) is needed.

[more]

denotes the quantity of goods transported from storage center to consumption center . The following is a mathematical model of the problem, where we try to minimize the total transportation cost :

,

, ,

, ,

is the total offer,

is the total request.

The transportation problem can be solved if . If , we introduce a fictional consumption center with the offer and transportation cost 0. if , we introduce a fictional storage center with the request and transportation cost 0.

The problem is shown for . The result shows a matrix whose row and column sums are the and . This matrix shows the quantity that each storage center should ship to each consumption center. If , we can obtain a 4×5 () matrix or a 5×4 () matrix, where the extra row or column corresponds to a fictional center.

[less]

Contributed by: Mandric Igor (Moldova State University) (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send