Solving the Subprime Loan Problem

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
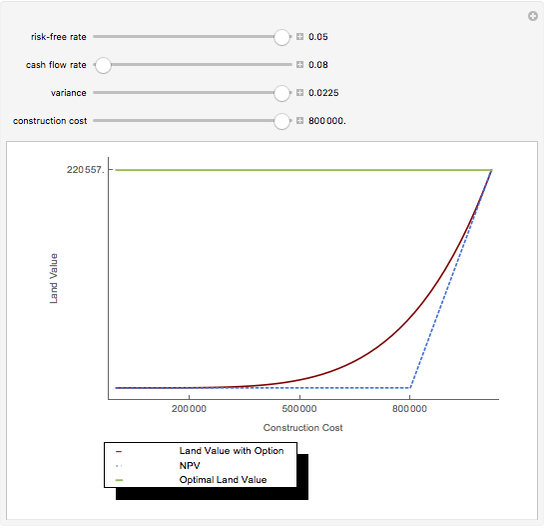
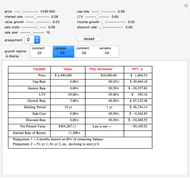
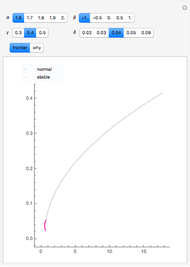
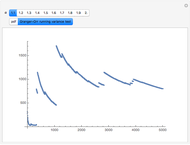
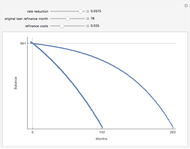
Much has been written about the boom-bust real estate cycle. Of late, the boom has been called a bubble and the bust has been called a credit crisis. There are some general conclusions that can be reached by following this market movement. Since most states do not allow lenders to hold borrowers personally liable for debt incurred to buy a home (and federal bankruptcy law makes it a practical impossibility in the remaining states), the borrower has the option to stop making payments and give the property to the lender in satisfaction of the debt. We can think of the borrower's option to make this decision as a "put option". If the home appreciates, the borrower has an incentive to keep making payments and reap the benefits of home ownership. If the opposite happens, the borrower can abandon, thereby "putting" the property to the lender, at a put option price equal to the then-outstanding balance of the loan.
[more]
Contributed by: Roger J. Brown (March 2011)
Reproduced by permission of Academic Press from Private Real Estate Investment ©2005
Open content licensed under CC BY-NC-SA
Snapshots
Details
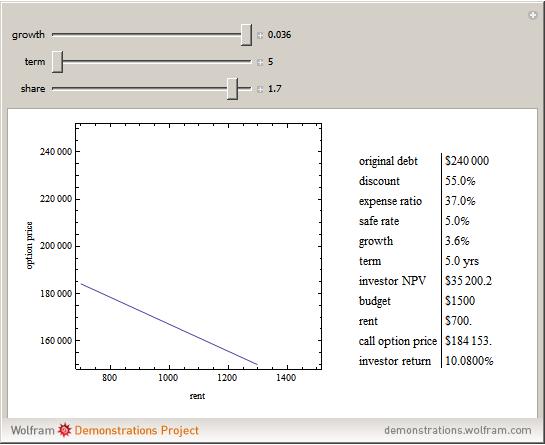
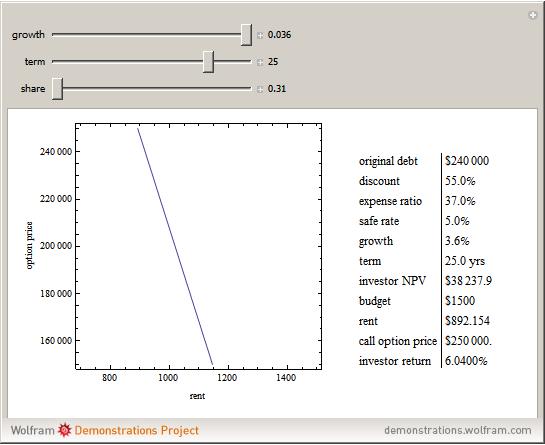
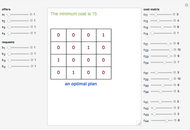
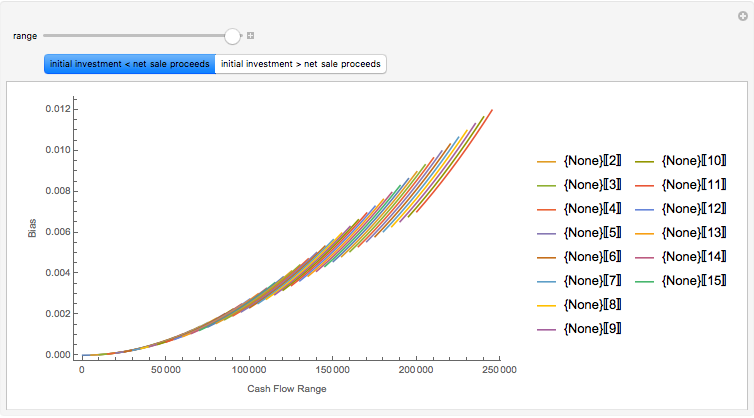
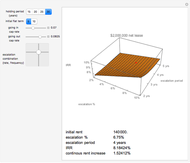
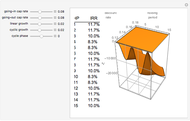
Note that a paternalistic lender, wishing to avoid a repeat of the first failure in a different form, can require all of the household budget to be paid monthly. The lender can then accumulate the sinking fund payments for the eventual purchase of the home via the call option. This activity is common for paying property taxes and insurance through a lender-maintained impound account. Although home ownership is usually not a decision centered on risk, the plot shows how risk can be "tilted" toward one party. Longer terms and lower growth assumptions make the proposition safer for the occupant; the alternative makes it more risky for that party.
A further variation would convert the lease option to a loan when the down payment was sufficient to convince the lender that, at the new loan-to-value ratio, the loan was well-secured. Including the income tax ramifications (mortgage interest is deductible and lease payments are not) adds mind-numbing complexity. The occupant can gain a tax advantage at any time. But the point at which that tax advantage is economically justified is a difficult, separate calculation.
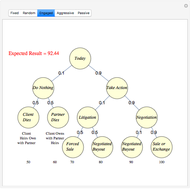
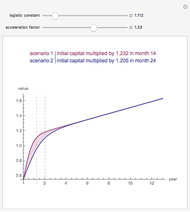
The goal of the maximization problem is to seek the optimal rent and call option value that maximizes the investor's net present value subject to the constraint that it is equal to the occupant's net present value multiplied by the sharing factor (initial value = 1, in which the investor and occupant share equally). The investor's yield is determined from these optima under the assumption that the call option will be exercised. As the sharing factor changes, the investor's yield will change, but the occupant's incentives (rent and call option price) also change in a way that makes exercise of the option more (sharing factor < 1) or less (sharing factor > 1) certain.
More information is available in Chapter Nine of Private Real Estate Investment and at mathestate.com.
R. J. Brown, Private Real Estate Investment: Data Analysis and Decision Making, Burlington, MA: Elsevier Academic Press, 2005.
Permanent Citation
"Solving the Subprime Loan Problem"
http://demonstrations.wolfram.com/SolvingTheSubprimeLoanProblem/
Wolfram Demonstrations Project
Published: March 7 2011