Motions of a Hexapod Robot

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
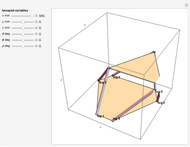
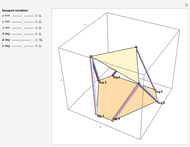
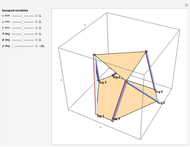
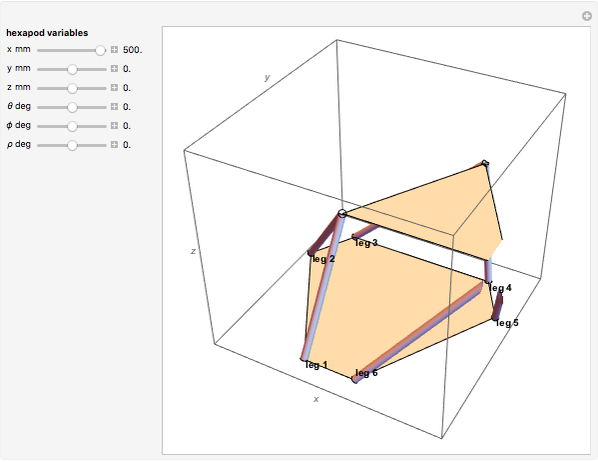
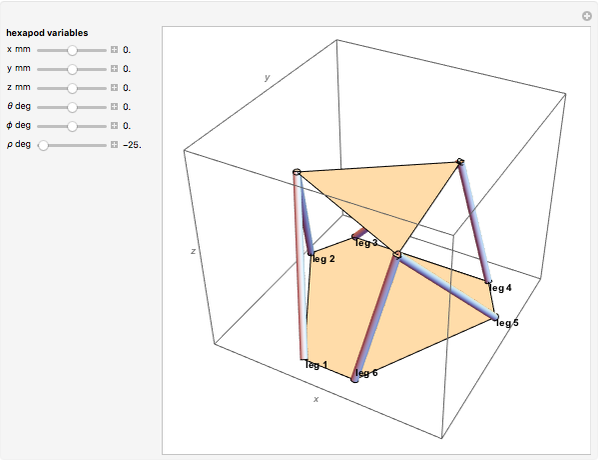
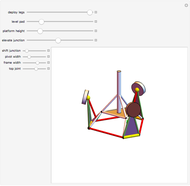
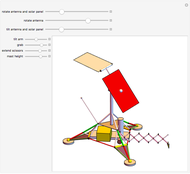
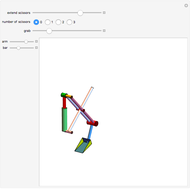
A Hexapod platform is a six-legged robot with six degrees of freedom. Also known as a Stewart–Gough platform, its principal advantages are a high load-to-weight ratio and the ability to precisely position heavy loads. Disadvantages include limitations on the range of motion.
Contributed by: Jim Fowler (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
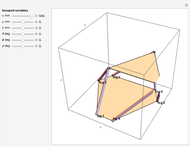
The Stewart–Gough or Hexapod platform consists of six extensible legs connecting a fixed base to a movable platform. The platform is capable of moving with six degrees of freedom, three translational and three rotational. The Inverse Problem in robotics, calculating the actuator coordinates (leg lengths) for a given platform orientation, is straightforward in this situation. Simple geometry is all that is needed to express the rotation and translation matrices. In a nutshell, the nominal platform coordinates of the legs are rotated and translated by the desired values. Then the leg lengths are calculated by simply taking the norm of the difference between the base and platform coordinates for each leg. This Demonstration uses homogeneous coordinates to combine the rotations and the translations into a single matrix operation.
Permanent Citation
"Motions of a Hexapod Robot"
http://demonstrations.wolfram.com/MotionsOfAHexapodRobot/
Wolfram Demonstrations Project
Published: March 7 2011