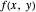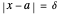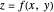Multivariable Epsilon-Delta Limit Definitions

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
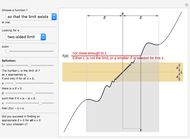
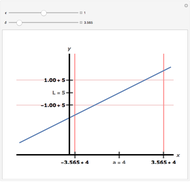
The definition of a limit:
The expression  is an abbreviation for: the value of the single-variable function
is an abbreviation for: the value of the single-variable function 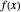 approaches
approaches 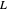
 as
as 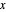 approaches the value
approaches the value 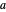 . More formally, this means that
. More formally, this means that 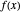 can be made arbitrarily close to
can be made arbitrarily close to  by making
by making 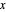 sufficiently close to
sufficiently close to 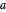 , or in precise mathematical terms, for each real
, or in precise mathematical terms, for each real 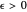 , there exists a
, there exists a  such that
such that 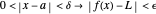 . In other words, the inequalities state that for all
. In other words, the inequalities state that for all  except
except 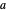 within
within  of
of 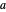 ,
, 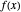 is within
is within  of
of 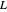 .
.
Contributed by: Spencer Liang (The Harker School) (March 2011)
Open content licensed under CC BY-NC-SA
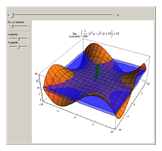
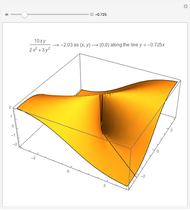
Snapshots
Details
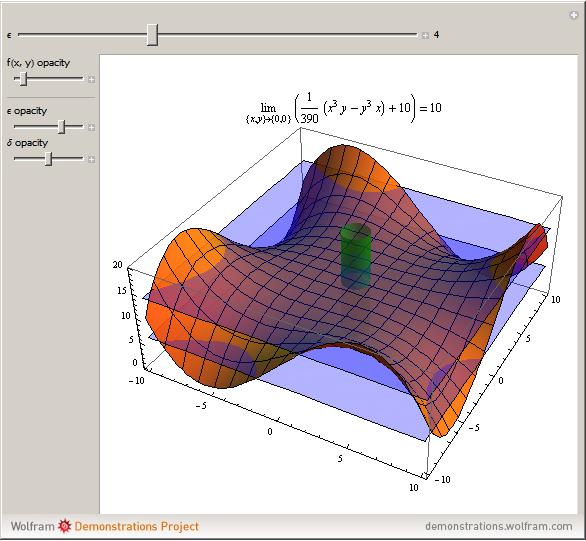
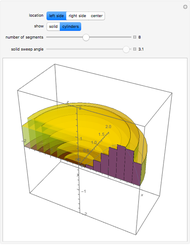
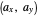 For the limit of a multivariable function, consider the two-variable function
For the limit of a multivariable function, consider the two-variable function 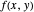 . (Note that the following extends to functions of more than just two variables, but for the sake of simplicity, two-variable functions are discussed.) The same limit definition applies here as in the one-variable case, but because the domain of the function is now defined by two variables, distance is measured as
. (Note that the following extends to functions of more than just two variables, but for the sake of simplicity, two-variable functions are discussed.) The same limit definition applies here as in the one-variable case, but because the domain of the function is now defined by two variables, distance is measured as 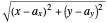 , all pairs
, all pairs 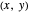 within
within  of
of 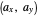 are considered, and
are considered, and 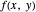 should be within
should be within  of
of  for all such pairs
for all such pairs 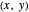 .
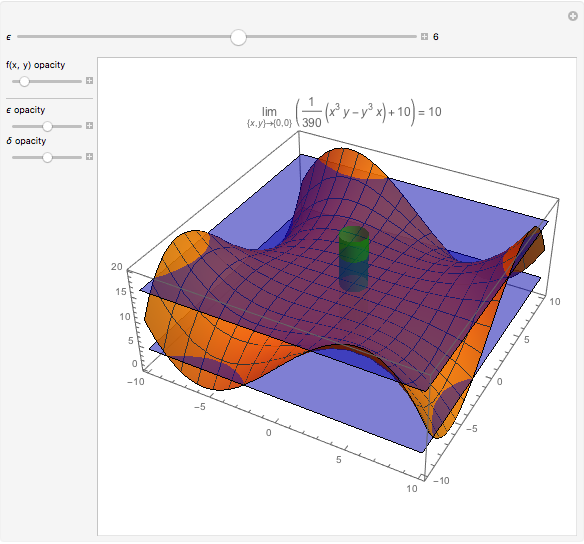
As an example, here is a proof that the limit of
.
As an example, here is a proof that the limit of 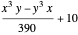 is 10 as
is 10 as 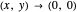 . Claim: for a given
. Claim: for a given 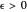 , choosing
, choosing 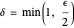 satisfies the appropriate conditions for the definition of a limit:
satisfies the appropriate conditions for the definition of a limit: 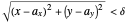 (the given condition) reduces to
(the given condition) reduces to  , which implies that
, which implies that 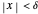 and
and 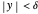 .
.
Now, 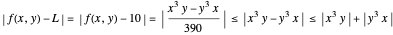 by the triangle inequality, and
by the triangle inequality, and 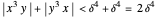 . If
. If  ,
, 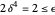 , and if
, and if 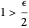 ,
, 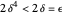 . Thus by the choice of
. Thus by the choice of  ,
, 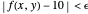 , and because
, and because  is arbitrary, an appropriate
is arbitrary, an appropriate  can be found for any value of
can be found for any value of  ; hence the limit is 10.
; hence the limit is 10.
Permanent Citation