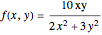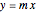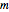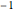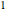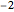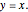Nonexistence of a Multivariable Limit

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
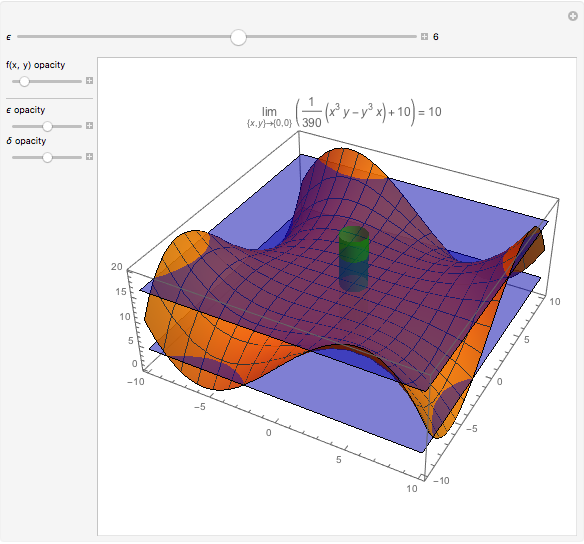
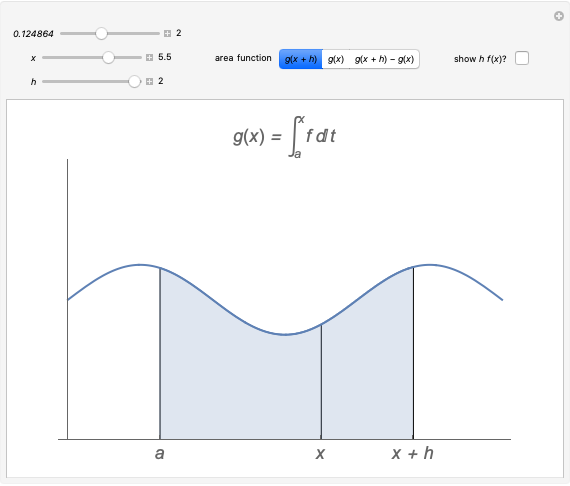
In multivariable calculus, a limit of a function 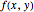 exists at a point
exists at a point 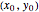 if and only if we can make
if and only if we can make 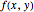 as close as we want to
as close as we want to 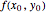 for all points
for all points 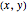 arbitrarily close to
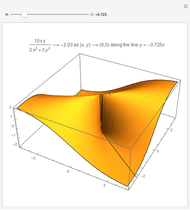
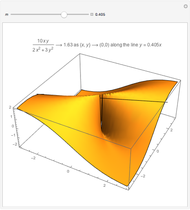
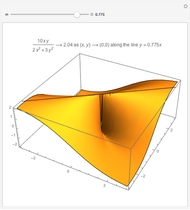
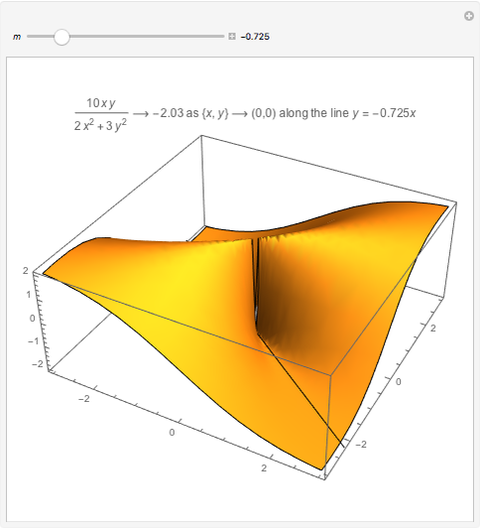
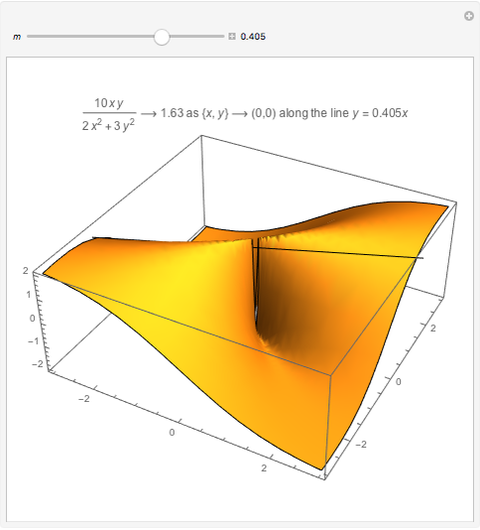
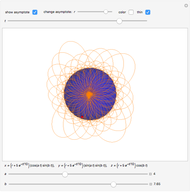
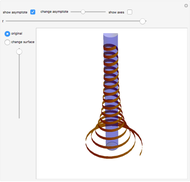
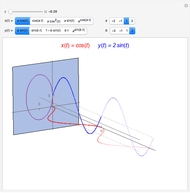
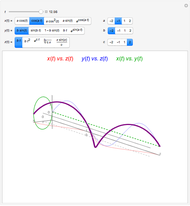
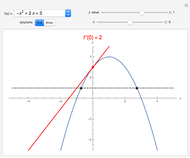
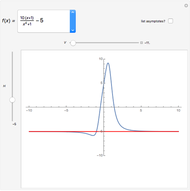
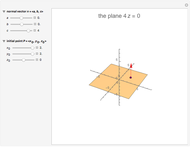
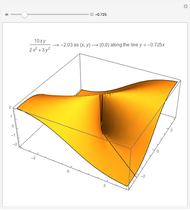
arbitrarily close to  One way to show that a limit does not exist (i.e. the definition fails) is to show that the function approaches different values from different directions. Akin to the notion of a one-sided limit in single-variable calculus, we consider the limit along a path in multivariable calculus. If the limit exists and is the same along all paths to
One way to show that a limit does not exist (i.e. the definition fails) is to show that the function approaches different values from different directions. Akin to the notion of a one-sided limit in single-variable calculus, we consider the limit along a path in multivariable calculus. If the limit exists and is the same along all paths to  then the limit of the function exists.
then the limit of the function exists.
Contributed by: Laura R. Lynch (May 2014)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Permanent Citation