Number-Theoretic Construction of Digital Circles

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
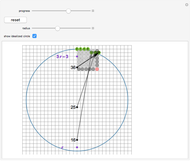
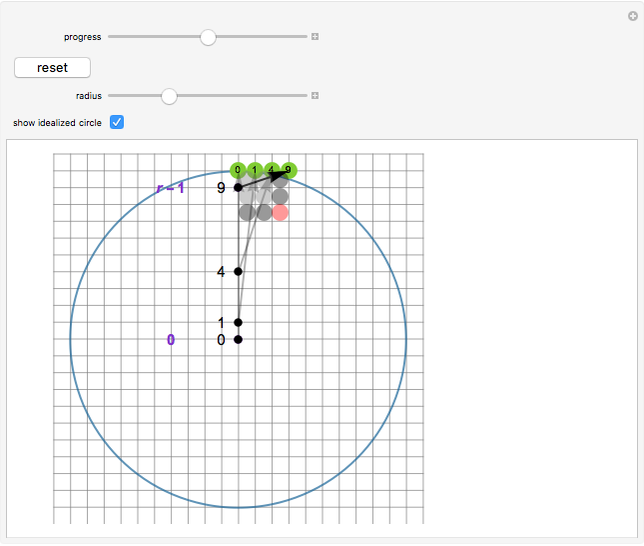
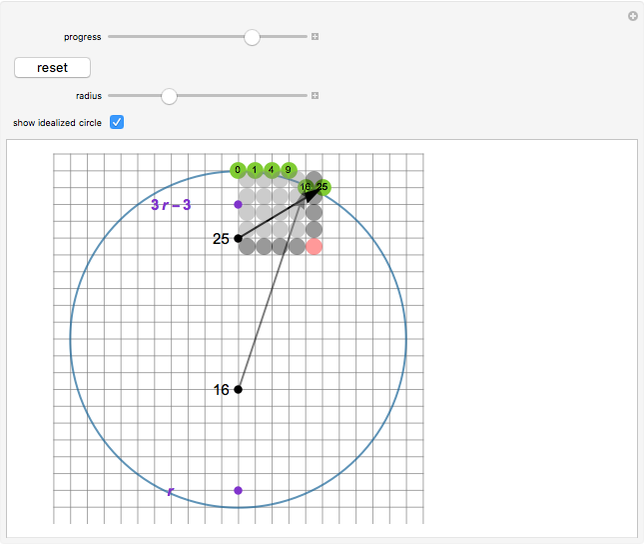
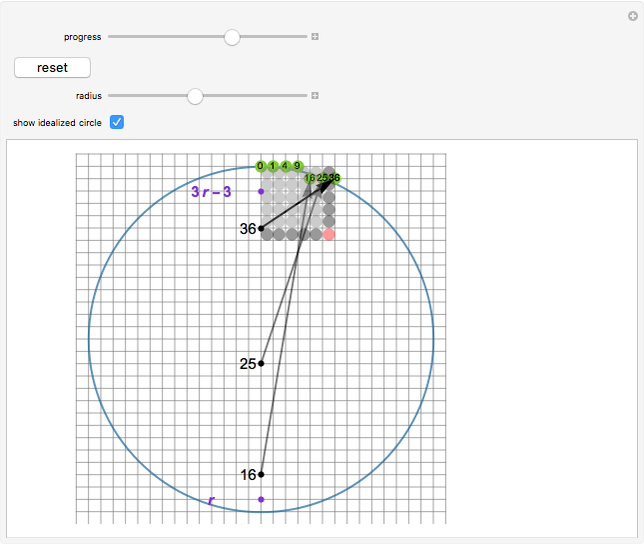
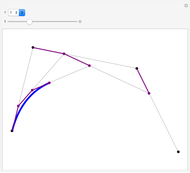
This is a construction of a digital circle. The algorithm used for the construction is based on number theory. It relates the run length to the number of square numbers in a certain interval that is calculated using a formula given in the Details section.
Contributed by: Aniket Jha (BTech Student IIT KGP), Partha Bhowmick (IIT KGP), and B. B. Bhattacharya (ISI Kolkata) (January 2009)
After work by: Partha Bhowmick and B. B. Bhattacharya
Open content licensed under CC BY-NC-SA
Snapshots
Details
The Demonstration has been prepared based on the paper:
P. Bhowmick and B. B. Bhattacharya, "Number-Theoretic Interpretation and Construction of a Digital Circle," Discrete Applied Mathematics, 156(12), 2008, pp. 2381–2399.
The main idea:
Let  be the radius of the circle and
be the radius of the circle and  the run number from the top (starting from 0).
the run number from the top (starting from 0).
The squares of the abscissas of the grid points lying on the digital circle corresponding to radius  and having ordinate
and having ordinate 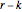 lie in the interval
lie in the interval 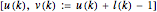 , where
, where 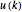 and
and 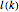 are defined by:
are defined by:
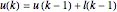 if
if 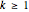
 if
if 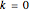
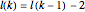 if
if 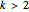
 if
if 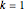
 if
if 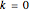 .
.
So the algorithm goes on calculating the consecutive square numbers, adding a point to the current run for each square number. It changes the run when the square number moves to the next interval.
It may be noted that the 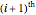 square number
square number  can be obtained easily (without using any multiplication) from the previous square number
can be obtained easily (without using any multiplication) from the previous square number 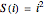 , since
, since 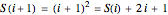 , which is equivalent to adding a "gnomon".
, which is equivalent to adding a "gnomon".
For details visit : http://dx.doi.org/10.1016/j.dam.2007.10.022
Permanent Citation