Linear Congruential Sequences

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
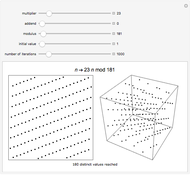
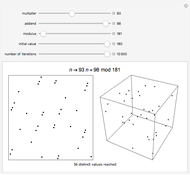
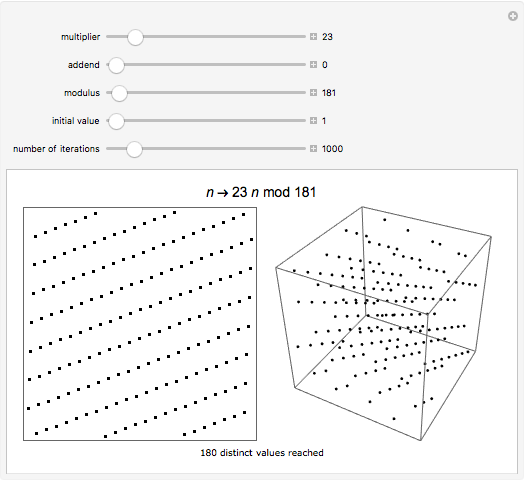
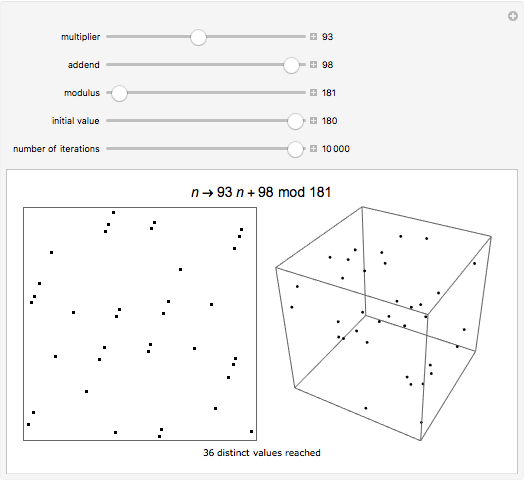
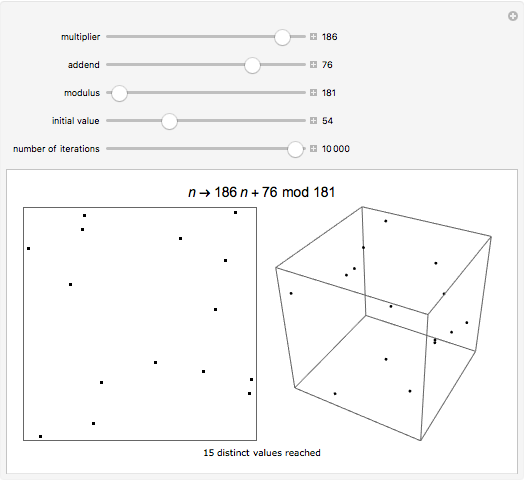
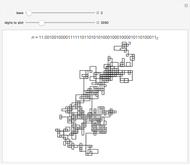
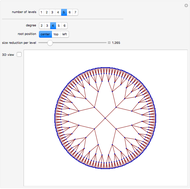
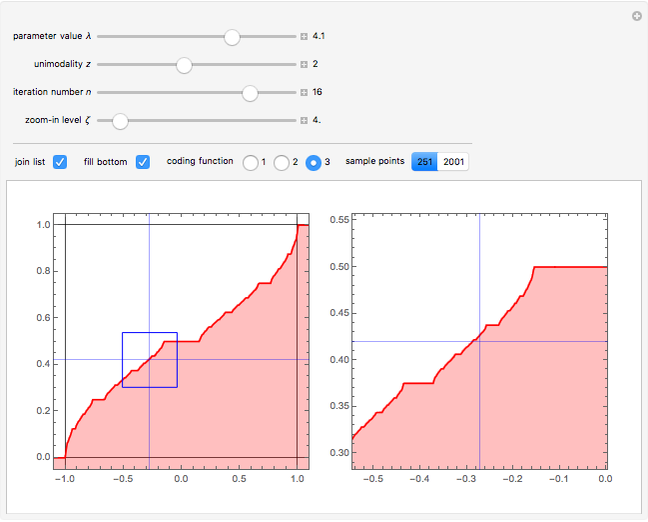
Linear congruential sequences are often used to make pseudorandom numbers. Try to pick moduli where the points lie as randomly as possible. Increasing the number of iterations often does not in fact increase the number of distinct points.
Contributed by: Stephen Wolfram (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
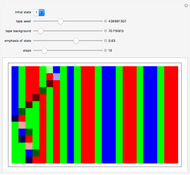
Each sequence starts with the number 1, then successively multiplies it by the specified multiplier, keeping only the rightmost 31 digits in the base 2 representation of the number obtained at each step. Multiplier 65539 was used as the random number generator on many computer systems, starting with mainframes in the 1960s. If the output from the generator were perfectly random, then in each case these points would be uniformly distributed. But, as the pictures demonstrate, stripes are visible in either two or three dimensions, or both.
Permanent Citation