Lattice Circles

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
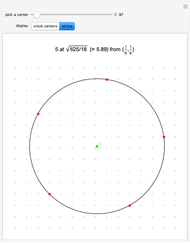
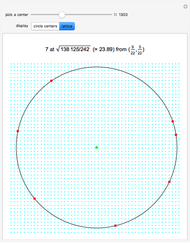
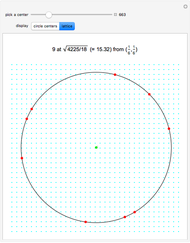
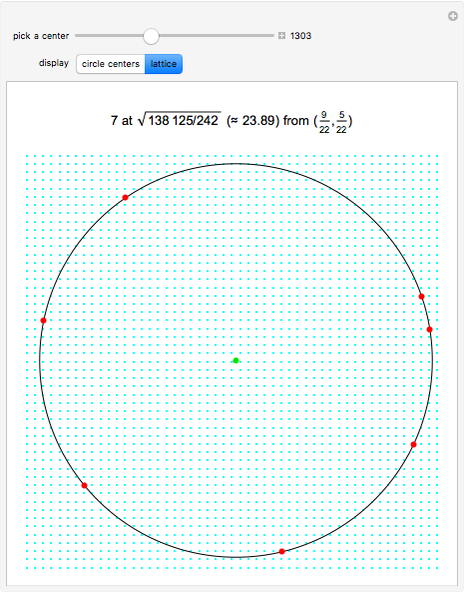
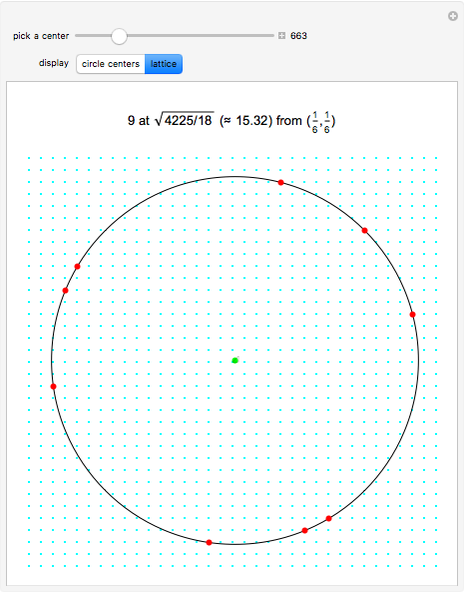
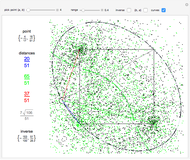
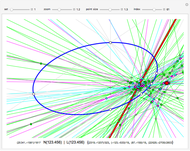
Any three noncollinear lattice points define a circle, which can be translated and (if necessary) reflected and/or rotated so that its center lies in the triangle  ,
,  ,
,  . Various lattice circles passing through four or more lattice points are precalculated for this Demonstration. For each center, the smallest lattice circle was selected that fits in a 60×60 grid and goes through exactly
. Various lattice circles passing through four or more lattice points are precalculated for this Demonstration. For each center, the smallest lattice circle was selected that fits in a 60×60 grid and goes through exactly  points.
points.
Contributed by: Ed Pegg Jr (March 2011)
Open content licensed under CC BY-NC-SA
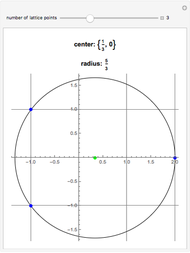
Snapshots
Details
For lattice circles going through exactly  points, the results below are minimal.
points, the results below are minimal.

Permanent Citation