Numerical Methods for Differential Equations

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
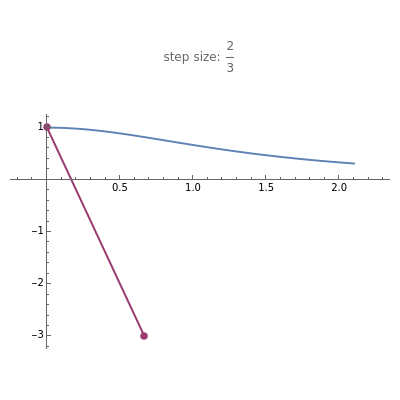
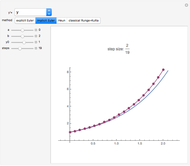
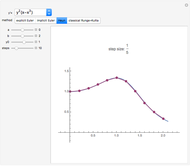
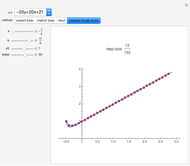
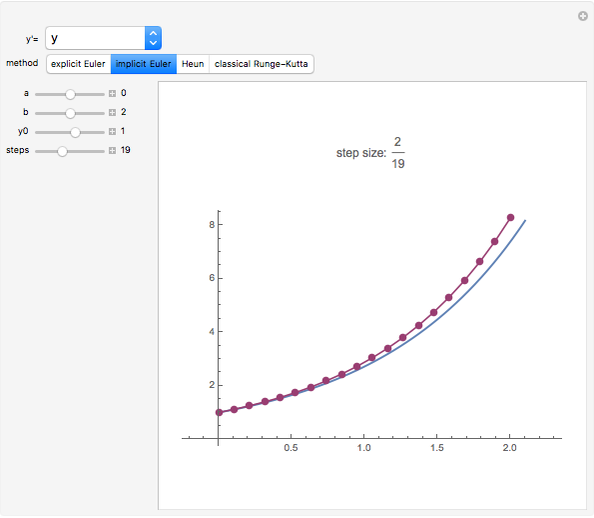
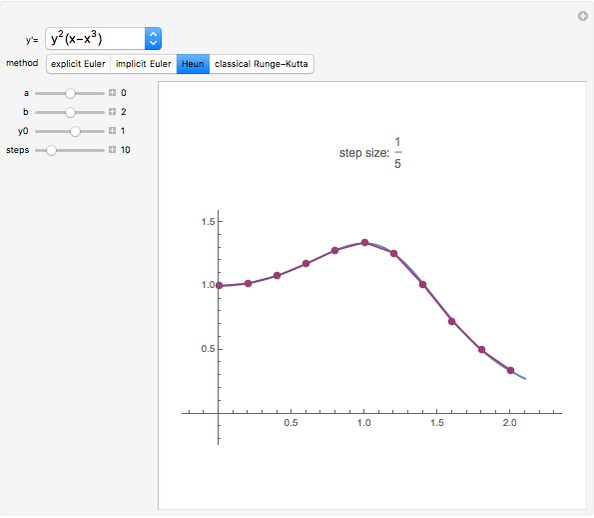
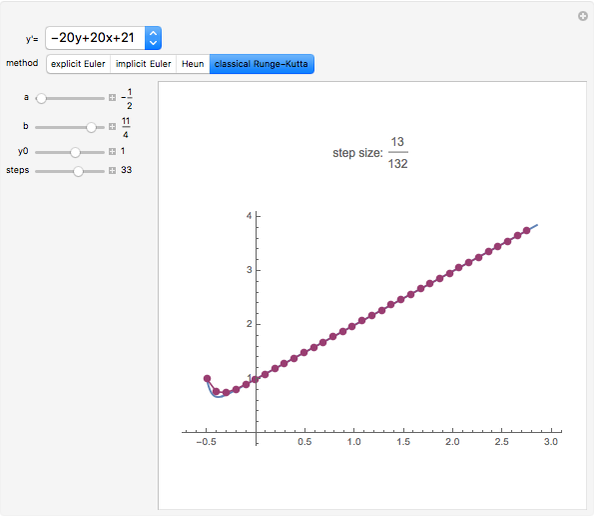
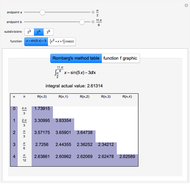
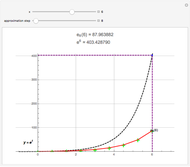
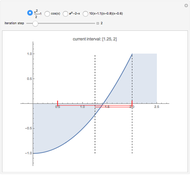
This Demonstration shows the exact and the numerical solutions using a variety of simple numerical methods for ordinary differential equations. Use the sliders to vary the initial value or to change the number of steps or the method.
Contributed by: Edda Eich-Soellner (February 2008)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The Demonstration shows various methods for ODEs:
* Euler's method is the simplest method for the numerical solution of an ordinary differential equation  . Starting from an initial point
. Starting from an initial point 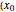 ,
, 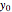 ) and dividing the interval [
) and dividing the interval [ ,
,  ] that is under consideration into
] that is under consideration into  steps results in a step size
steps results in a step size 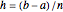 ; the solution value at point
; the solution value at point  is recursively computed using
is recursively computed using 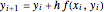 ,
,  .
.
* Implicit Euler method
* Heun's method
* classical Runge-Kutta method of order 4
The last right-hand side given belongs to a stiff equation, such that the behavior of the method for this type of equation can be studied. See M. Heath, Scientific Computing: An Introductory Survey, New York: McGraw-Hill, 2002.
Note that Mathematica provides all of the methods outlined here and many others as part of the NDSolve framework. In contrast to the simple implementations used here, Mathematica uses more advanced methods which are e.g. equipped with error estimation and step size selection strategies as well as a stiffness switching; see Mathematica's advanced documentation for NDSolve.
Permanent Citation
"Numerical Methods for Differential Equations"
http://demonstrations.wolfram.com/NumericalMethodsForDifferentialEquations/
Wolfram Demonstrations Project
Published: February 26 2008