Bisection Method

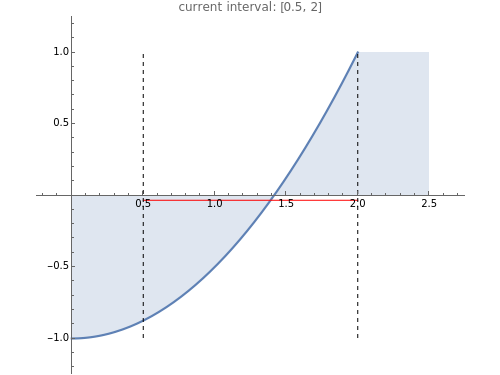
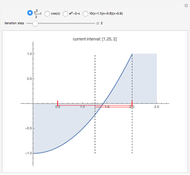
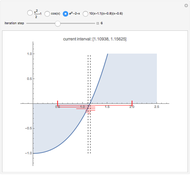
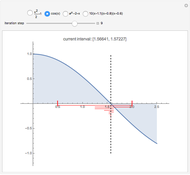
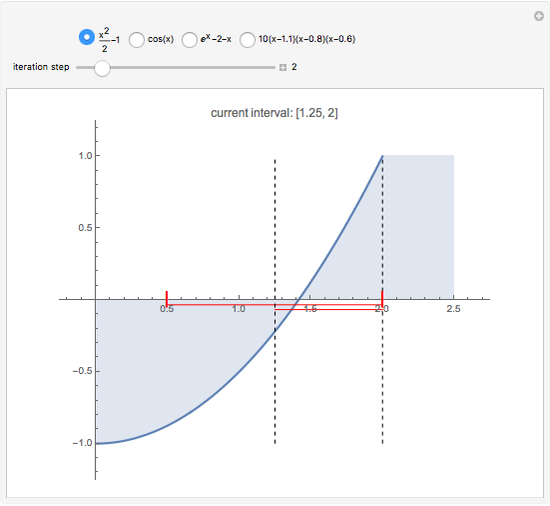
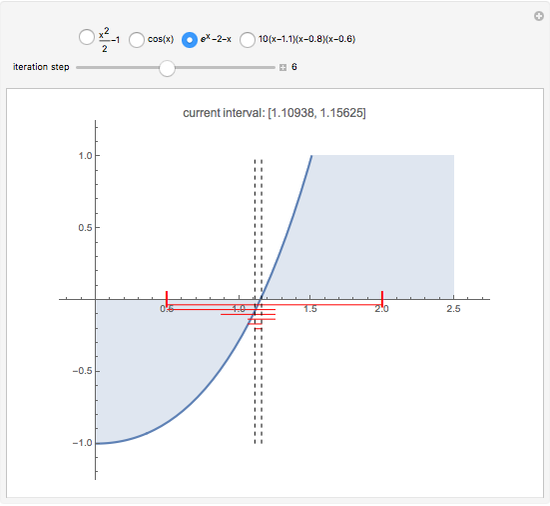
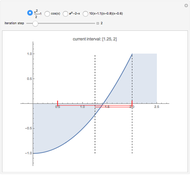
This Demonstration shows the steps of the bisection root-finding method for a set of functions. You can choose the initial interval by dragging the vertical, dashed lines. Each iteration step halves the current interval into two subintervals; the next interval in the sequence is the subinterval with a sign change for the function (indicated by the red horizontal lines). The method always converges to a root of if is continuous and and have opposite sign.