Numerical Evaluation of Some Definite Integrals

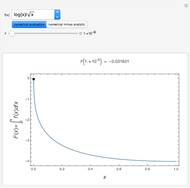
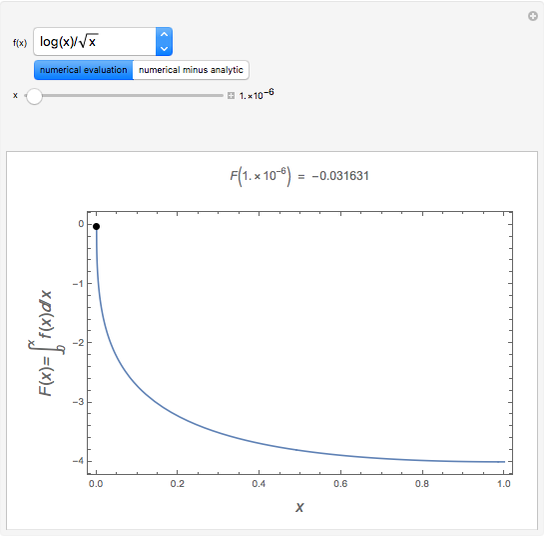
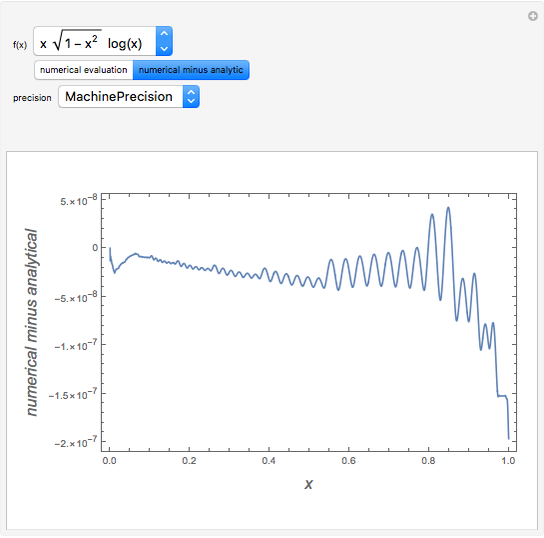
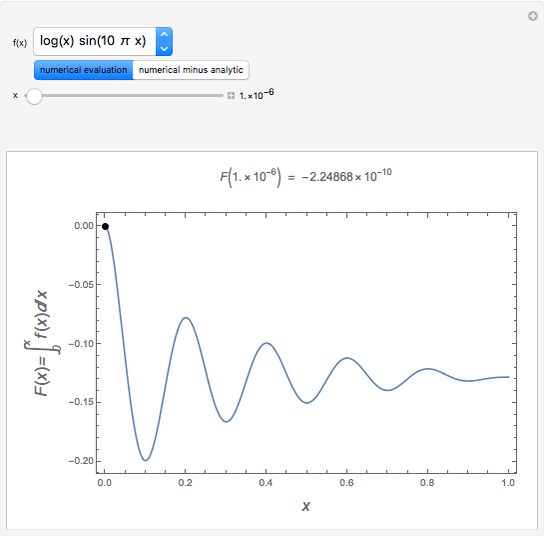
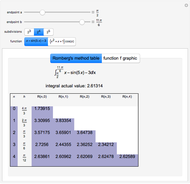
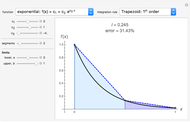
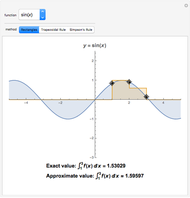
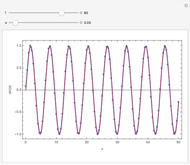
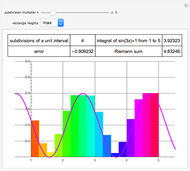
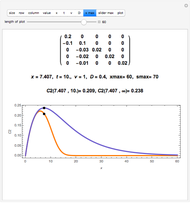
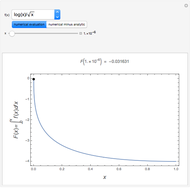
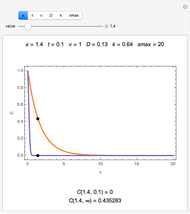
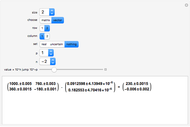
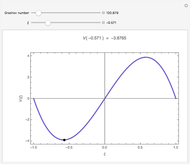
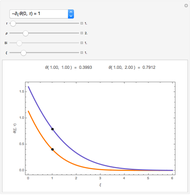
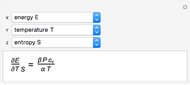
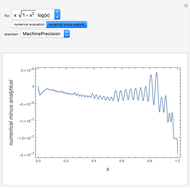
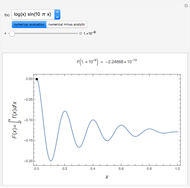
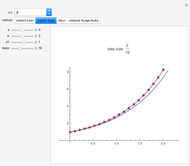
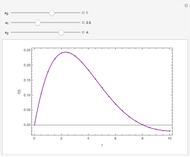
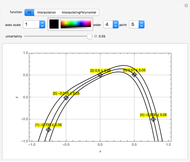
This Demonstration shows a trick for computing the definite integral numerically in a given interval of its upper bound using Mathematica. Instead of using NIntegrate we use the function NDSolve. Five test functions are borrowed from reference [1]. Four of these test functions have a singular point at . You can plot the analytic solutions of the test integrals as well as the difference of the numerical and analytic solutions as a function of the upper bound variable for different working precisions. The black point on the curve gives the function value when the slider position is at . At the right endpoint these values coincide with the values given in the reference in the details.