Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

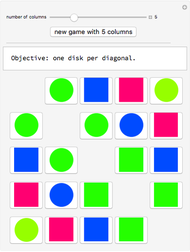
One Disk Per Diagonal

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

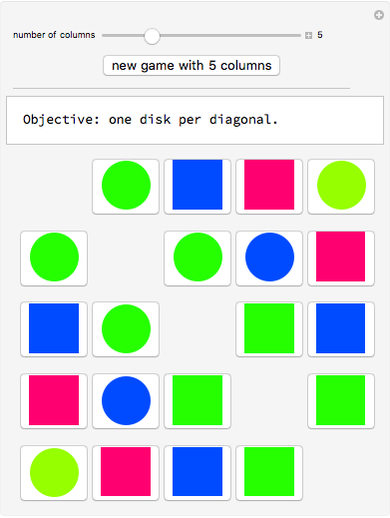
Each diagonal parallel to the main diagonal (which is blank) is colored with one color. The objective is to have exactly one disk on each diagonal, which is equivalent to finding the adjacency matrix of a graceful graph.

[more]

Clicking the button in the row and column first swaps the shapes (but not the colors) in rows and , and then swaps the shapes (but not the colors) in columns .

[less]

Contributed by: Wai-Shun Cheung (December 2011)
Open content licensed under CC BY-NC-SA

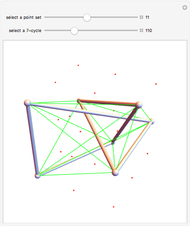
Snapshots

Details

Graceful[n] generates a 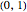-matrix with zero main diagonal and a unique 1 on each of its parallel diagonals. Essentially this is an adjacency matrix of an 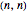-edge graceful graph, hence the name.

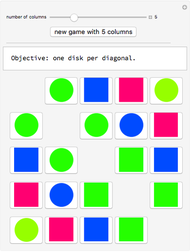
Snapshot 1 (the rectangles are the 0's and the disks are the 1's): Once the "new game" button is hit, a new matrix 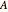is generated. Then we apply a permutation matrix so that the resulting matrix 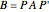gives a puzzle to solve.

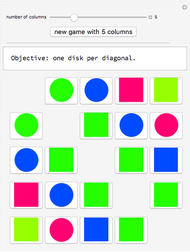
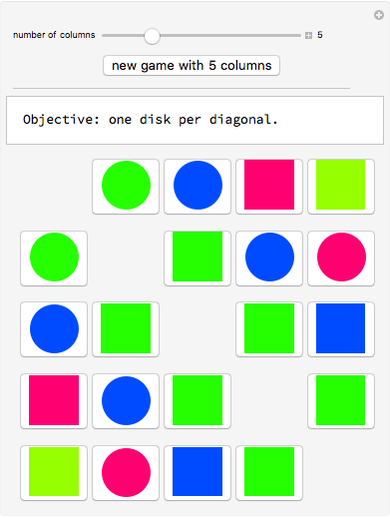
Snapshot 2: Click on a grid element to apply a transposition matrix; this is the effect of Swap[A,i,j]. In the snapshot, we click on position (3,5) or (5,3) to get 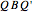, where 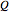corresponds to the transposition (3,5).

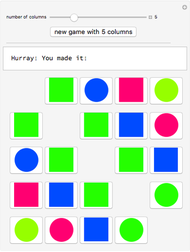
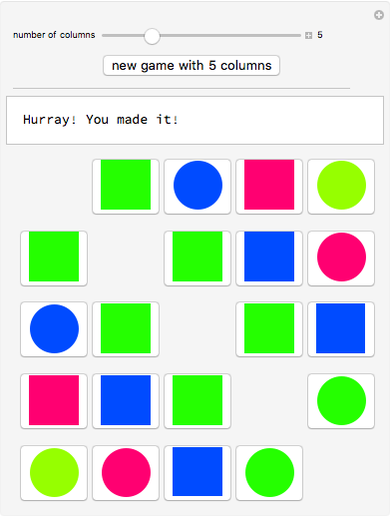
Snapshot 3: Continue the process to get back the "one disk per diagonal" structure. The answer is not unique.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send