Devilish Mazes

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
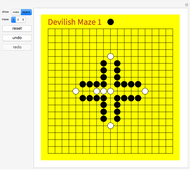
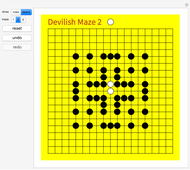
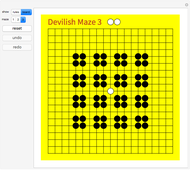
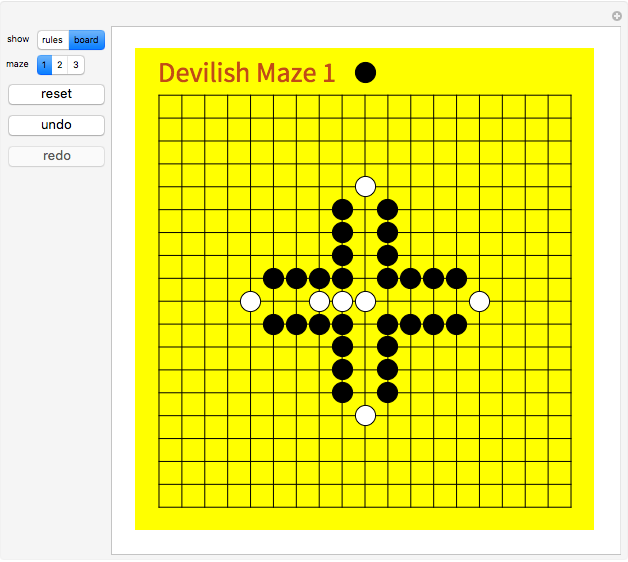
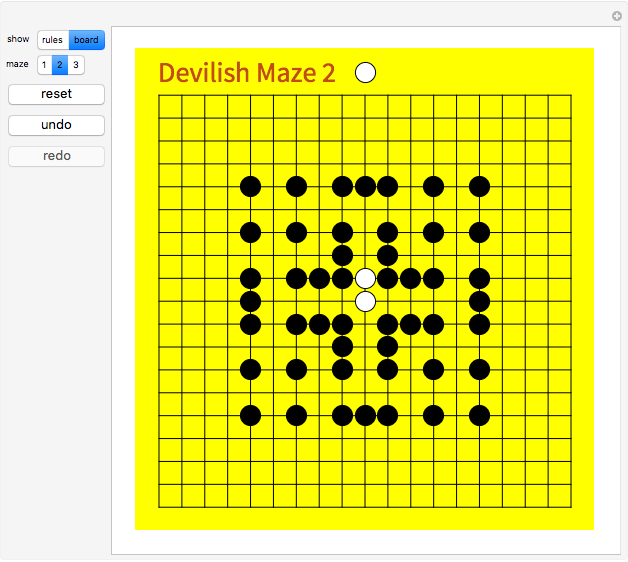
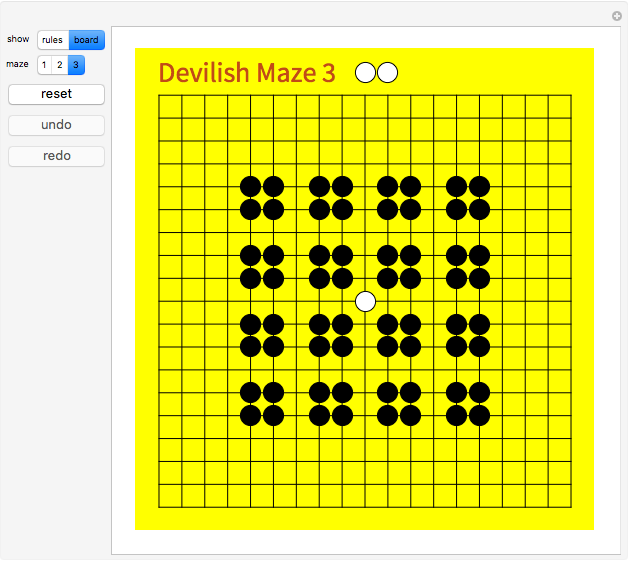
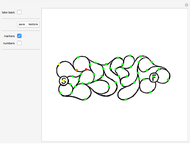
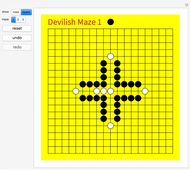
This Demonstration offers three interesting two-person games on a 19×19 Go board. Click "rules" to get an explanation of how to play. The Demonstration illustrates how to create an intuitive interface for playing board games, and how to use the built-in Mathematica graph algorithms to determine when the game is over.
Contributed by: Tom Verhoeff (February 2014)
(Eindhoven University of Technology)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The graphical user interface involves virtual stones on all empty intersections. Such a virtual stone is completely transparent, unless the mouse passes over it (Mouseover), in which case the opacity is increased to show a partly transparent stone of the appropriate color. That stone is also turned into a button, whose action makes the move of playing the stone on that location.
The game result is determined by considering two graphs, both having the board lines as edges. The first graph has the white stones as vertices. If there exists a path in this graph from the white stone in the center to a target location, then White has won. The second graph has the white stones plus the empty locations as vertices. If there exists a path in the second graph from the center to a target, then White can still win. Of course, when White can no longer win, Black has won (by successfully containing White).
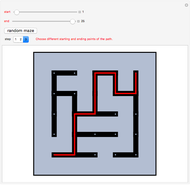
Maze 1 was taken from [1]. Mazes 2 and 3 were taken from [2].
References
[1] Y. Yasuda, Let's Play Go!: A Simple Introduction to the Game of Go, Richmond, VA: Slate & Shell, 2004.
[2] Y. Yu-Chia, A Scientific Introduction to Go, Santa Monica, CA: Yutopian Enterprises, 2002.
Permanent Citation
"Devilish Mazes"
http://demonstrations.wolfram.com/DevilishMazes/
Wolfram Demonstrations Project
Published: February 3 2014