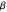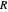Optimal Patch Exploitation

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
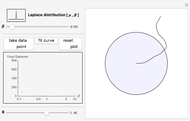
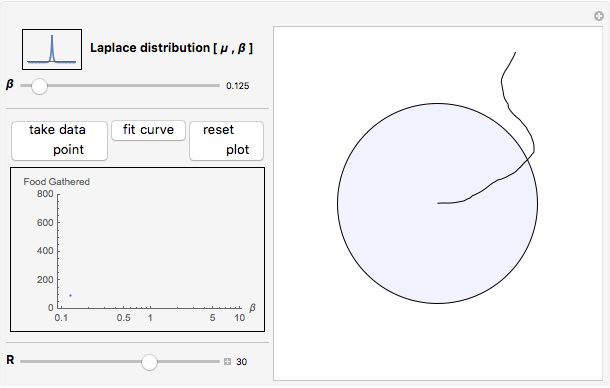
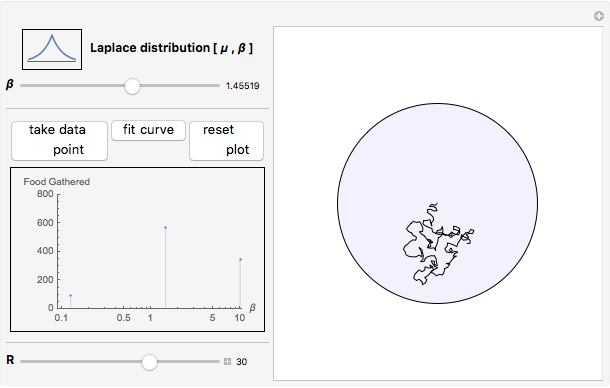
This Demonstration is an investigation into the efficiency of an animal (or organism) feeding in a circular food patch (gray circle) while traveling in a concatenated string of unit-length forward "hops". In between each hop, the animal executes precise turns through specific angles of all sizes that are chosen randomly from the probability distribution pictured in the upper left-hand corner. Food is distributed evenly inside the food patch, and every particle of food along the trajectory (the black line starting from the center of the patch) is "gathered" by the forager. Note that the animal does not find food in any place where it has previously traveled, or when it is outside of the food patch.
[more]
Contributed by: Nathan D. Dees (March 2011)
After work by: Nathan D. Dees, Sonya Bahar, and Frank Moss
Open content licensed under CC BY-NC-SA
Snapshots
Details
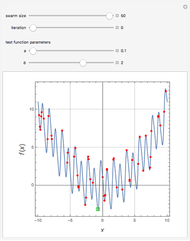
This model is based on work presented in the Journal of Theoretical Biology by Dees et al. (2008). The paper explored the efficiency of different distributions of turning angles, 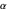 , used in the hop, pause, turn through an angle, hop again... sequences of modeled and real zooplankton Daphnia while the animals foraged for food. In the wild, Daphnia feed on patches of phytoplankton or algae near the surface of the water, moving in a roughly two-dimensional plane. Interestingly, when these tiny creatures are observed foraging in a laboratory, various species of Daphnia exhibit Laplacian distributions of turning angles,
, used in the hop, pause, turn through an angle, hop again... sequences of modeled and real zooplankton Daphnia while the animals foraged for food. In the wild, Daphnia feed on patches of phytoplankton or algae near the surface of the water, moving in a roughly two-dimensional plane. Interestingly, when these tiny creatures are observed foraging in a laboratory, various species of Daphnia exhibit Laplacian distributions of turning angles, 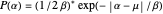 , where
, where 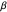 determines the "width" of the distribution, and
determines the "width" of the distribution, and  identifies the peak of the distribution, typically occurring at 0 radians (symbolizing equal numbers of left-hand and right-hand turns, Garcia et al. (2007).) Even more remarkable than the similarities found in the overall shapes of the distributions were the congruences in the values of
identifies the peak of the distribution, typically occurring at 0 radians (symbolizing equal numbers of left-hand and right-hand turns, Garcia et al. (2007).) Even more remarkable than the similarities found in the overall shapes of the distributions were the congruences in the values of 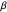 that characterized them. Since similar values of
that characterized them. Since similar values of 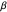
 (~1.06 radians) were found for six different species of Daphnia and two different age groups, the authors hypothesized that the distributions of turning angles used by foraging Daphnia might be a large factor in the fitness of the animals, and that the widths of these distributions might have evolved to a specific range over millions of years of natural selection.
(~1.06 radians) were found for six different species of Daphnia and two different age groups, the authors hypothesized that the distributions of turning angles used by foraging Daphnia might be a large factor in the fitness of the animals, and that the widths of these distributions might have evolved to a specific range over millions of years of natural selection.
In the Demonstration, a value of 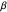 is selected via the uppermost slider, and then a string of turning angles is chosen randomly from a Laplacian distribution whose shape is described by this
is selected via the uppermost slider, and then a string of turning angles is chosen randomly from a Laplacian distribution whose shape is described by this 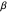 . Note that the distribution pictured above the slider is truncated to the range
. Note that the distribution pictured above the slider is truncated to the range  , since the maximum amount of turn allowed for an agent is a complete 180° rotation to the left (
, since the maximum amount of turn allowed for an agent is a complete 180° rotation to the left (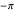 ) or to the right (
) or to the right (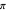 ). This range covers all possible headings. At the highest values of
). This range covers all possible headings. At the highest values of 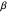 , the truncated distribution resembles a uniform and uncorrelated distribution with every angle having nearly equal probabilities of being selected to be used in the trajectory. Smaller values of
, the truncated distribution resembles a uniform and uncorrelated distribution with every angle having nearly equal probabilities of being selected to be used in the trajectory. Smaller values of 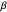 result in a very thin distribution, limiting the random selection to just a few lower-valued choices.
result in a very thin distribution, limiting the random selection to just a few lower-valued choices. 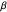 , therefore, symbolizes the amount of variation, jitter, or noise that exists in the group of turning angles which make up the random trajectory. (This follows from the mathematical definition of
, therefore, symbolizes the amount of variation, jitter, or noise that exists in the group of turning angles which make up the random trajectory. (This follows from the mathematical definition of 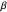 —it is directly proportional to the standard deviation of
—it is directly proportional to the standard deviation of 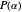 .) Smaller values of
.) Smaller values of 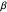 result in random sets full of smaller-valued turning angles (closer to 0 radians), and therefore more straight-line motion in the trajectory. Larger values of
result in random sets full of smaller-valued turning angles (closer to 0 radians), and therefore more straight-line motion in the trajectory. Larger values of 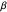 beget sets of turning angles with plenty of larger-valued angles (closer to
beget sets of turning angles with plenty of larger-valued angles (closer to  radians) that lead to sharper turns and therefore more compact, localized trajectories.
radians) that lead to sharper turns and therefore more compact, localized trajectories.
Snapshot 1: excessive numbers of smaller turning angles will quickly carry a forager from the center of the food patch and beyond its border, where there will be no food
Snapshot 2: excessive numbers of larger turning angles will cause a forager to repeatedly travel back and forth upon its own path, again gathering very little food
There must be an optimum amount of variability in the turning angles a forager uses to gather food. The optimum value of 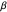 hinges upon the theory of stochastic resonance, in which some function of noise (in this case, the standard deviation of the turning angles,
hinges upon the theory of stochastic resonance, in which some function of noise (in this case, the standard deviation of the turning angles, 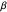 ) is added to a physical or biological system (here, modeled agents foraging for food), and as a result, optimizes that system. For more information, see Wiesenfeld and Moss (1995).
) is added to a physical or biological system (here, modeled agents foraging for food), and as a result, optimizes that system. For more information, see Wiesenfeld and Moss (1995).
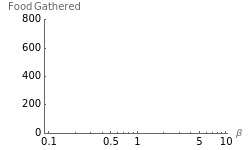
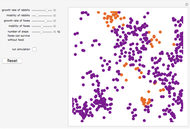
Snapshot 3: as data is collected at a given food patch size, determined by the radius, 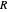 , peaks in food gathered should emerge at the most advantageous values of
, peaks in food gathered should emerge at the most advantageous values of 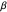
The results of this algorithm are stochastic—the trajectories and the data points collected will never look the same from trial to trial. But, through the performance of many trials, a consistently advantageous value of 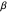 should be revealed by the peaks in the fitted curves. The optimum amount of noise should shift as the size of the food patch is adjusted. For example, a trajectory that extends to the edges of a food patch of radius 40 units will provide very little nourishment if used in a food patch of radius 10 units—the forager will have left the patch too quickly.
should be revealed by the peaks in the fitted curves. The optimum amount of noise should shift as the size of the food patch is adjusted. For example, a trajectory that extends to the edges of a food patch of radius 40 units will provide very little nourishment if used in a food patch of radius 10 units—the forager will have left the patch too quickly.
N. D. Dees, S. Bahar, R. Garcia, and F. Moss, "Patch Exploitation in Two Dimensions: From Daphnia to Simulated Foragers," Journal of Theoretical Biology, 252(1), 2008 pp. 69-76.
R. Garcia, F. Moss, A. Nihongi, J. R. Strickler, S. Göller, U. Erdmann, L. Schimansky-Geier, and I. M. Sokolov, "Optimal Foraging by Zooplankton within Patches: The Case of Daphnia," Mathematical Biosciences, 207, 2007 pp. 165-188.
K. Wiesenfeld and F. Moss, "Stochastic Resonance and the Benefits of Noise: From Ice Ages to Crayfish and SQUIDs," Nature, 373, 1995 pp. 33-36.
Permanent Citation