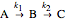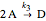Particle Swarm Optimization Applied to the van de Vusse Mechanism

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
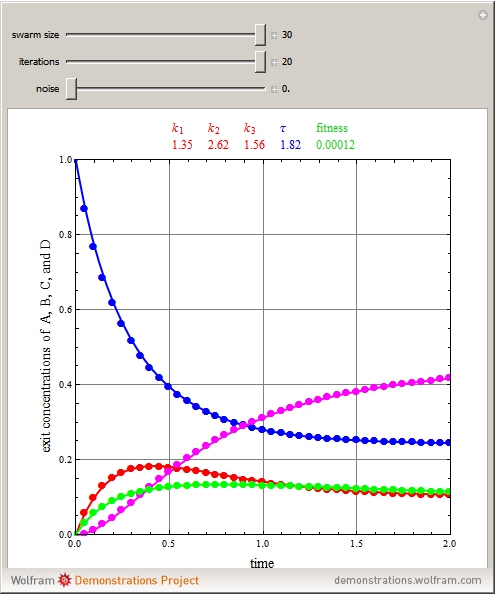
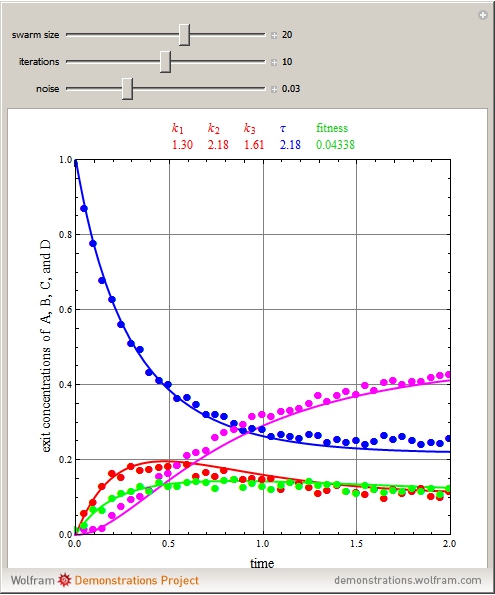
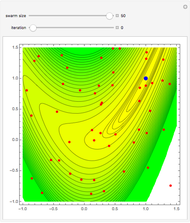
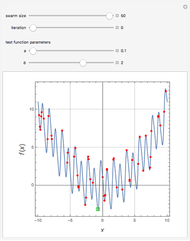
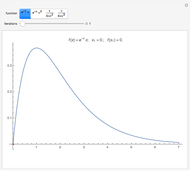
Consider the following complex reaction scheme (called the van de Vusse mechanism), taking place in a continuous stirred-tank reactor (CSTR) with a residence time  and rate constants
and rate constants 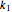 ,
,  ,
,  :
:
Contributed by: Housam Binous, Ahmed Bellagi, Ali Kh. Al-Matar, and Brian G. Higgins (November 2014)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Particle swarm optimization (PSO) resulted from the pioneering work of Kennedy and Eberhart [1, 2]. PSO algorithms mimic the social behavior patterns of organisms that live and interact within large groups, such as swarms of bees.
References
[1] J. Kennedy and R. Eberhart, "Particle Swarm Optimization," in Proceedings of the 1995 International Conference on Neural Networks, Vol. 4, New York: IEEE Press, 1995 pp. 1942–1948. doi:10.1109/ICNN.1995.488968.
[2] J. Kennedy and R. Eberhart, Swarm Intelligence, San Francisco: Morgan Kaufmann Publishers, 2001.
Permanent Citation