Orbit of a Launched Satellite

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
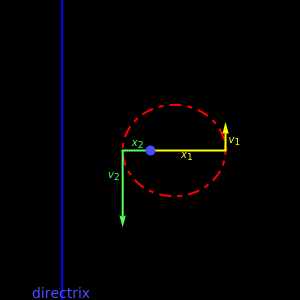
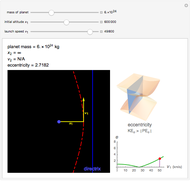
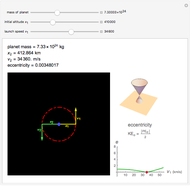
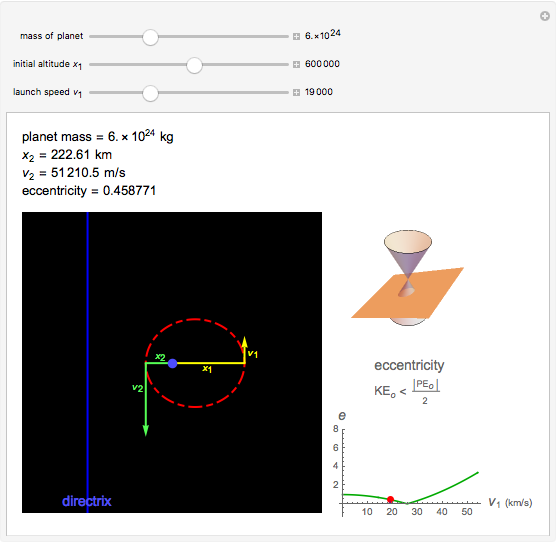
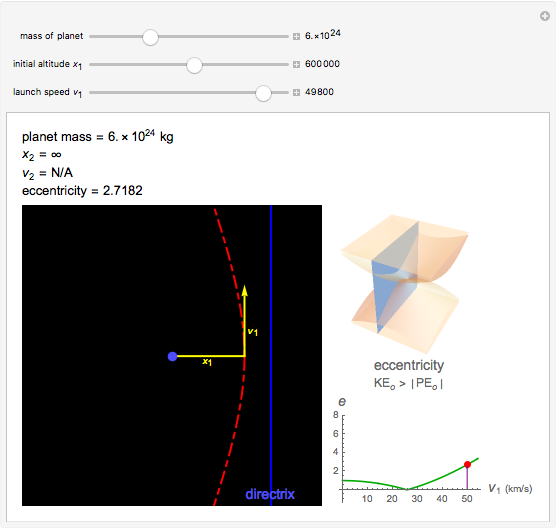
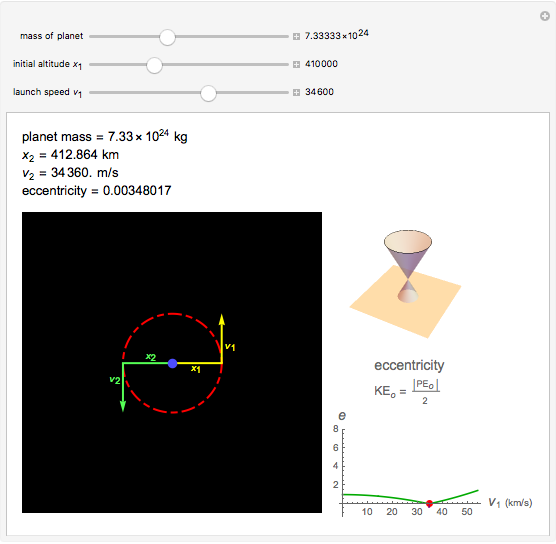
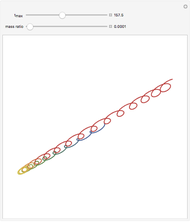
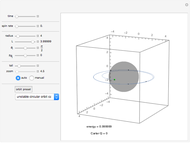
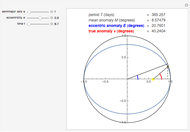
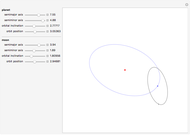
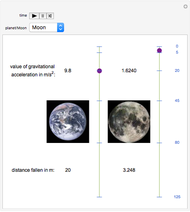
Kepler observed that the path of a satellite in an orbit around a heavy mass traces out an ellipse. More generally, an orbit in the absence of a third body is always a conic section (i.e., an ellipse, parabola, or hyperbola). For a parabolic orbit, the eccentricity equals 1, for any value of the initial launch speed. This speed along with the planet's mass, the initial altitude and the gravitational constant, 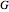 , determine the eccentricity of the conic section traced by the satellite's orbit. If the orbit is closed, then the speed is always greatest at the smallest distance from the planet and smallest at the greatest distance from the planet. This is derived from conservation of angular momentum.
, determine the eccentricity of the conic section traced by the satellite's orbit. If the orbit is closed, then the speed is always greatest at the smallest distance from the planet and smallest at the greatest distance from the planet. This is derived from conservation of angular momentum.
Contributed by: Victor Hakim & Bryce Kriegman (April 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
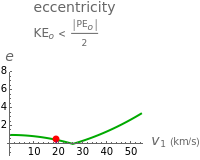
For a circular or elliptical orbit, the potential energy is twice the negative of kinetic energy, as a result of the virial theorem. The eccentricity  is zero for a circular orbit and
is zero for a circular orbit and 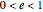 for an elliptical orbit. For a hyperbolic orbit
for an elliptical orbit. For a hyperbolic orbit 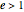 . When
. When  , the shape of the orbit degenerates to a parabola, moving at the escape velocity.
, the shape of the orbit degenerates to a parabola, moving at the escape velocity.
In this Demonstration, the largest eccentricity is about 21. Also note that the conic image will not generate for eccentricities greater than about 10.
Permanent Citation