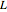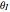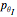3D Kerr Black Hole Orbits

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
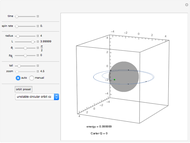
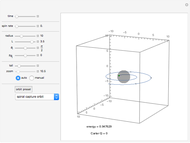
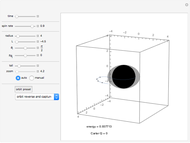
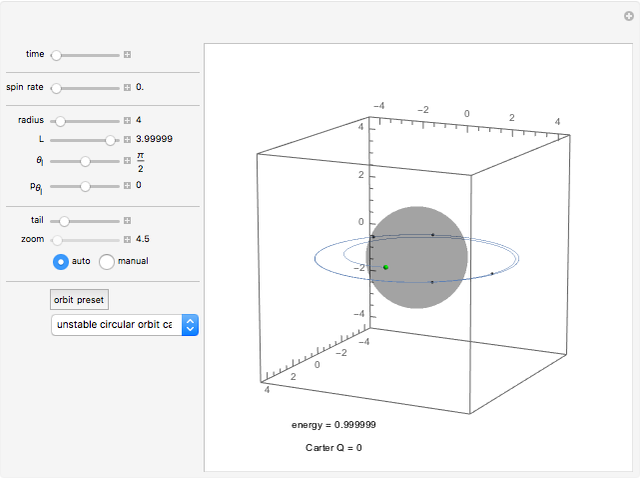
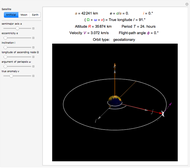
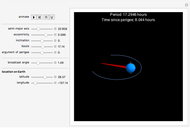
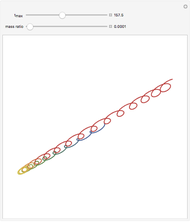
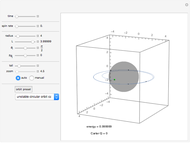
When a rotating star collapses to become a black hole it continues spinning. The grey region, called the ergosphere, is where the hole's spin drags space in the direction of the hole's rotation so strongly that nothing can move counter to the spin. The black hole is spinning like a top, with the spin axis pointing upwards.
[more]
Contributed by: David Saroff (March 2011)
Open content licensed under CC BY-NC-SA
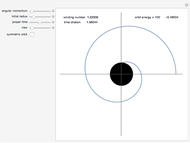
Snapshots
Details
Thanks to Janna Levin for criticism and suggestions. The Hamiltonian from which the equations of motion were derived is in appendix A of Levin and Perez-Giz, "A Periodic Table for Black Hole Orbits", arXiv:0802.0459.
Permanent Citation