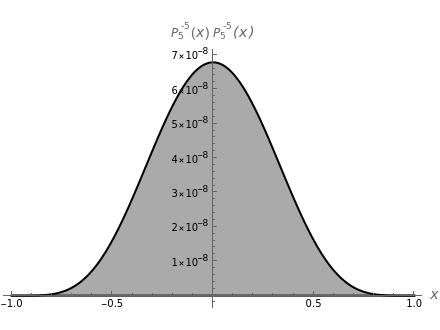
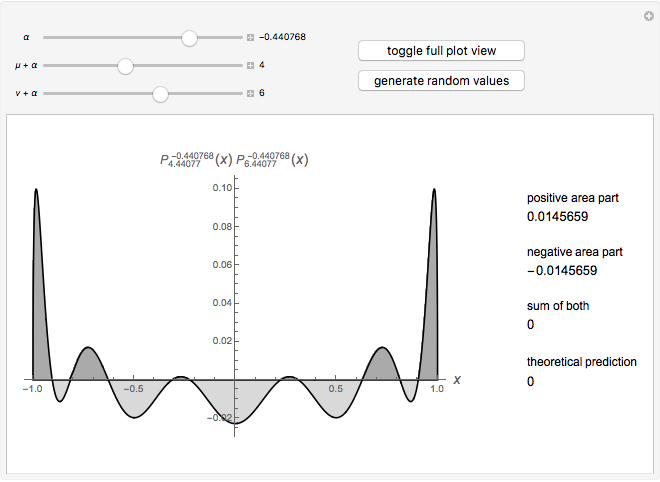
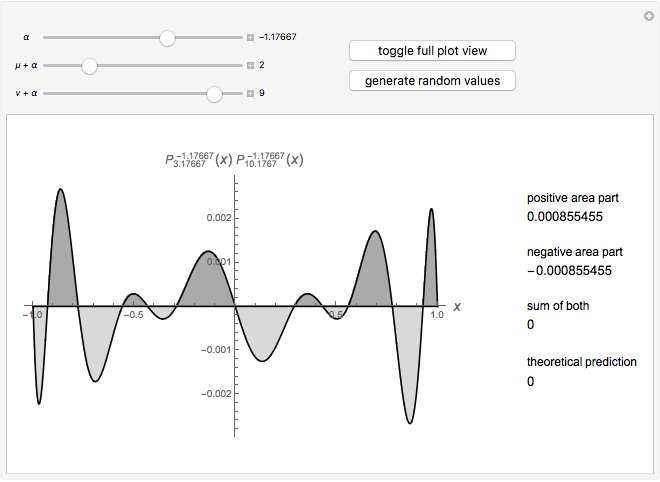
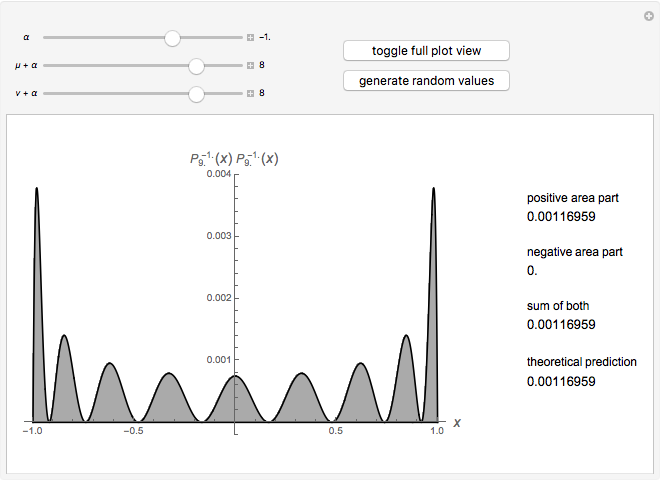
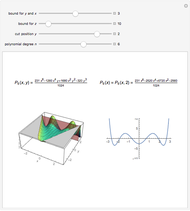
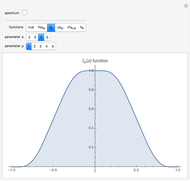
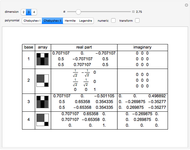
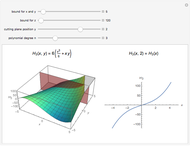
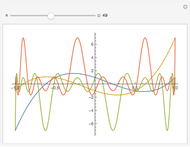
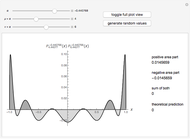
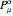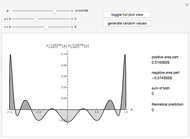
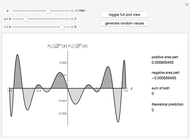
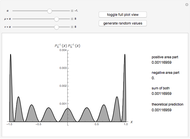
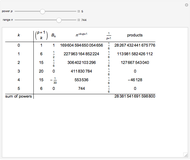
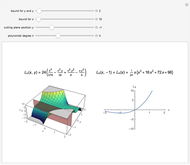
This Demonstration shows an unusual orthogonality relation for Legendre functions of the first kind . In contrast to the well-known situation of integer degree and integer order (associated Legendre polynomials), in this case both degree and order are allowed to take noninteger real values. 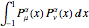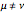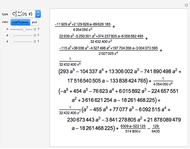For fixed , these functions satisfy an orthogonality relation, according to which is 0 whenever is equal to 2 if and 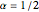, and is given by the formula 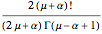in any other case.