Pairwise Axes Rotations in Factor Analysis

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
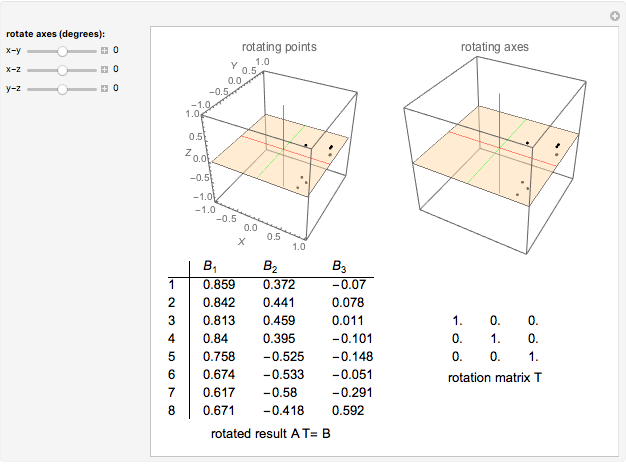
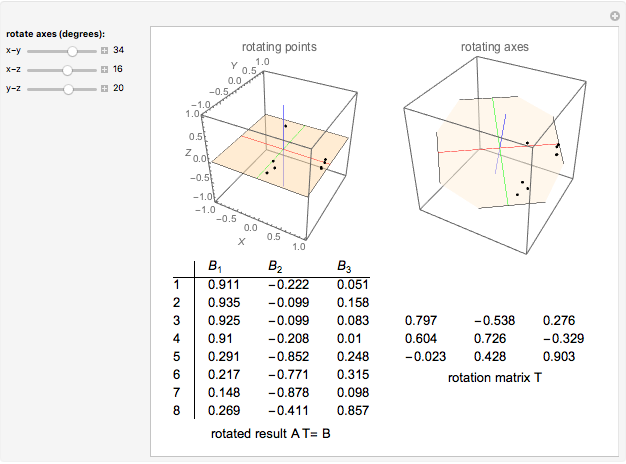
A correlation matrix  for eight physical variables is approximated by
for eight physical variables is approximated by  with
with  , where
, where 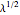 is the diagonal matrix of the square roots of the three largest eigenvalues of
is the diagonal matrix of the square roots of the three largest eigenvalues of  and
and  is an 8×3 matrix that contains the associated eigenvectors as columns. Using pairwise orthogonal rotations
is an 8×3 matrix that contains the associated eigenvectors as columns. Using pairwise orthogonal rotations  , elements of
, elements of  are adjusted so that the squared values in
are adjusted so that the squared values in 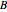 have a simple structure; that is, each row of
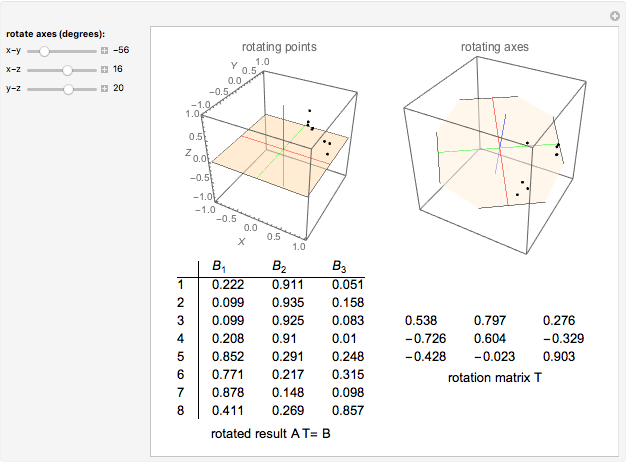
have a simple structure; that is, each row of 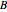 has only one high value and the other values are relatively small in comparison. A solution approximating the results of the Varimax algorithm for orthogonal rotations (H.F. Kaiser, 1958) is given by these three rotations:
has only one high value and the other values are relatively small in comparison. A solution approximating the results of the Varimax algorithm for orthogonal rotations (H.F. Kaiser, 1958) is given by these three rotations:  -
-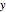 : 34° (or -56°),
: 34° (or -56°),  -
- : 16°,
: 16°, 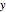 -
- : 20°.
: 20°.
Contributed by: Steve Hunka (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
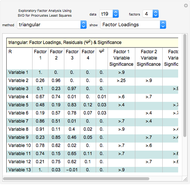
The eight physical variables are: (1) height, (2) arm span, (3) forearm length, (4) lower leg length, (5) weight, (6) bitrochanteric diameter, (7) chest girth, and (8) chest width. The tabular output includes the rotated matrix 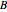 and the rotation matrix
and the rotation matrix  . Variable clusters are (1,2,3,4), (5,6,7), and (8).
. Variable clusters are (1,2,3,4), (5,6,7), and (8).
Permanent Citation