Periodic Heat Kernel

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
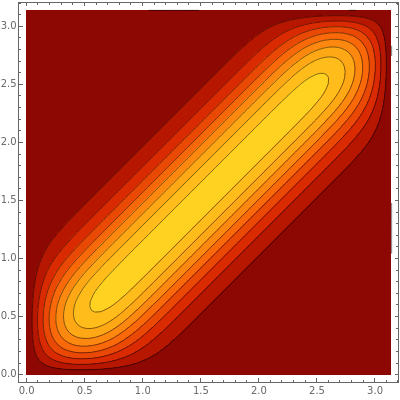
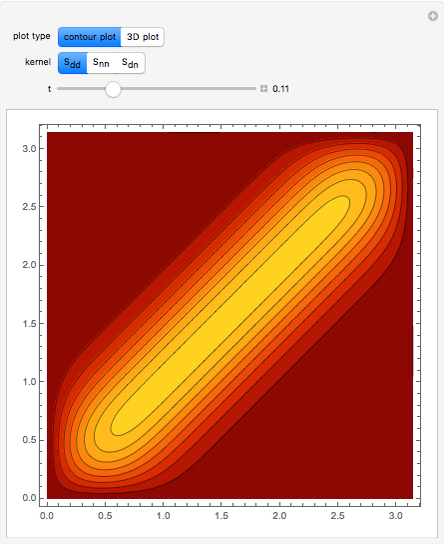
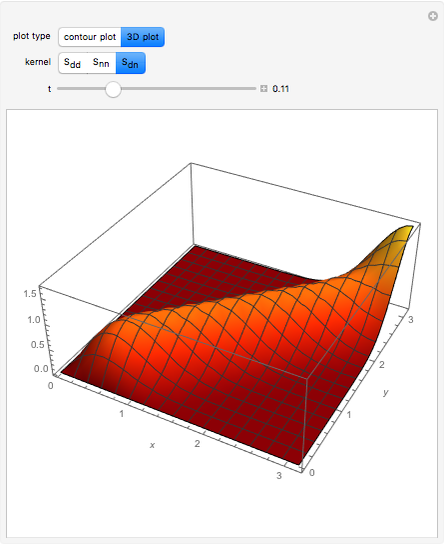
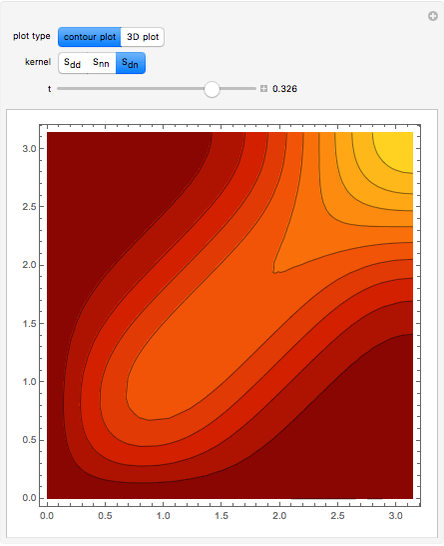
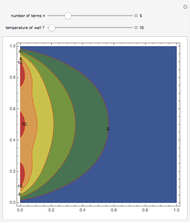
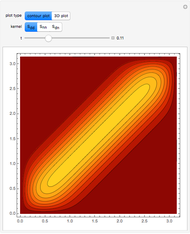
This Demonstration illustrates the localization of the heat kernel as  tends to zero on a finite interval with homogeneous boundary conditions of type Dirichlet, Neumann, or Cauchy (mixed).
tends to zero on a finite interval with homogeneous boundary conditions of type Dirichlet, Neumann, or Cauchy (mixed).
Contributed by: William O. Bray (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The periodic heat kernel is simply the periodization of the standard Gaussian heat kernel on the real line. Its explicit form is:
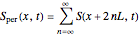 ,
,
where 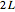 is the period and
is the period and 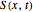 is the normalized Gaussian. Given the homogeneous heat equation on a finite interval with homogeneous Dirichlet, Neumann, or mixed boundary conditions, the heat kernel for the problem can be expressed in terms of the periodic heat kernel via the method of reflection. For example, in the case of Dirichlet boundary conditions,
is the normalized Gaussian. Given the homogeneous heat equation on a finite interval with homogeneous Dirichlet, Neumann, or mixed boundary conditions, the heat kernel for the problem can be expressed in terms of the periodic heat kernel via the method of reflection. For example, in the case of Dirichlet boundary conditions,
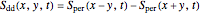 .
.
Integrating the resulting kernel in the  variable against the initial data provides the solution to the initial value problem. This form of the heat kernel is particularly useful when
variable against the initial data provides the solution to the initial value problem. This form of the heat kernel is particularly useful when  is small, in which case it approximates a delta function.
is small, in which case it approximates a delta function.
Permanent Citation