Mathematica MathWorld Wolfram Science More »

Unsteady Heat Transfer over a Porous Flat Plate


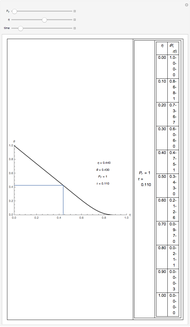
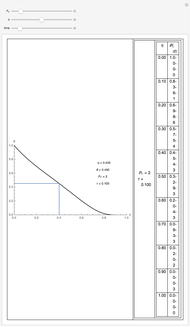
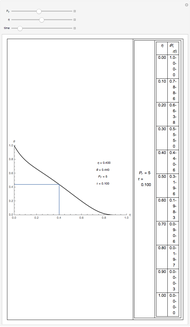
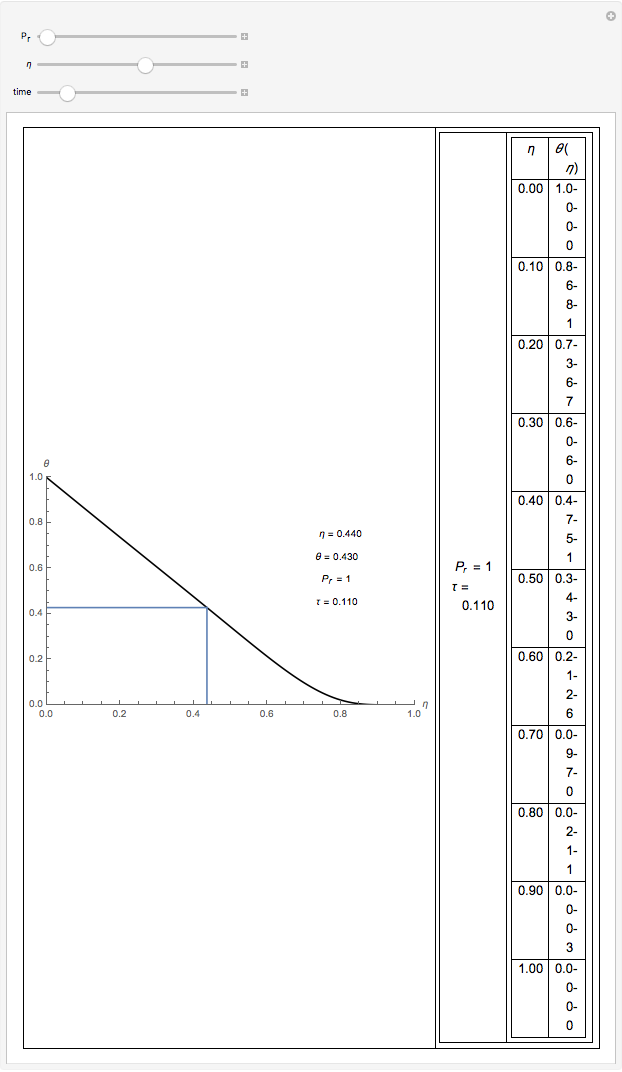
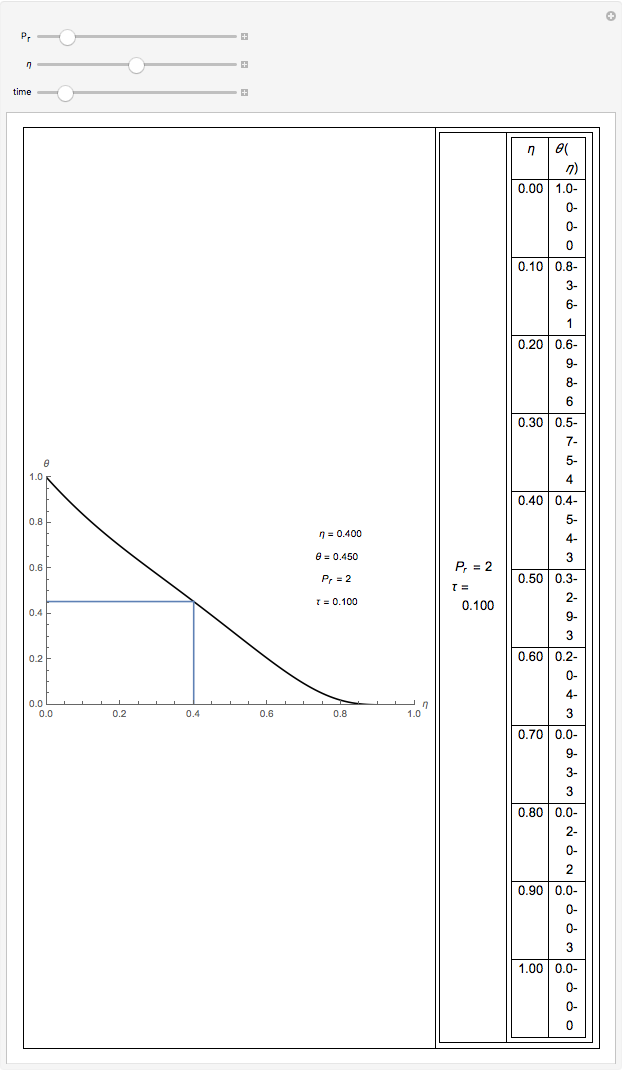
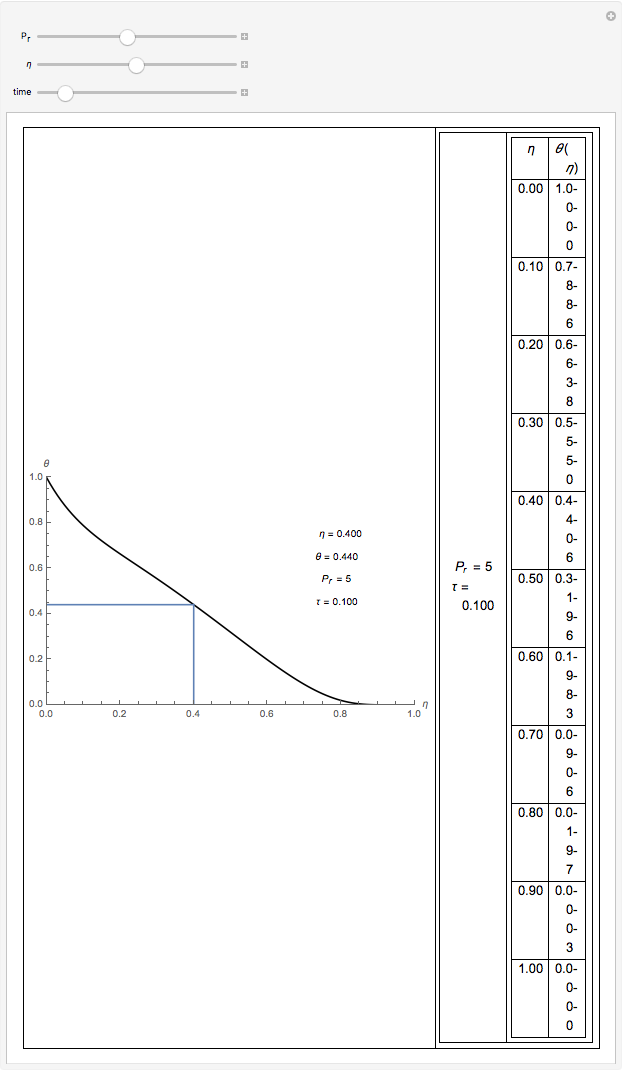
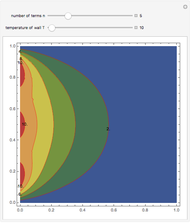
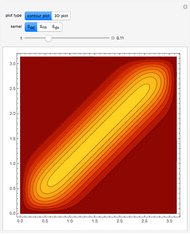
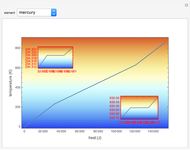
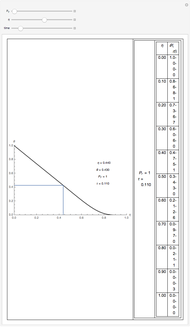
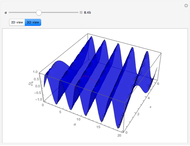
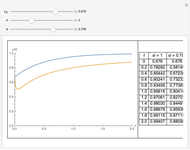
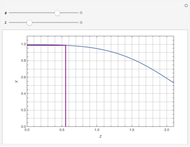
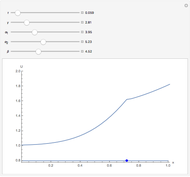
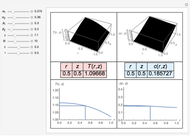
	This Demonstration gives a numerical solution of the energy equation for the temperature distribution in viscous flow past a porous flat plate. The solution uses a finite difference method.


	Contributed by: Jorge Gamaliel Frade Chávez

The dimensionless transformed energy equation that describes the temperature field is

with the boundary conditions

;

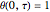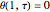and the initial condition

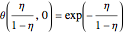Here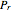

is Prandtl's number,

is non-dimensional temperature,

is dimensionless time, and

is dimensionless position.

Reference: R. S. Agarwal and M. Rani, "Numerical Solution of Unsteady Heat Transfer over a Porous Flat Plate," Indian Journal of Pure and Applied Mathematics, 16(6), 1985 pp. 647–659.

Report an issue »

	Source page:
	Email	Name (optional)
	Occupation (optional)	Organization (optional)
	I use Mathematica often occasionally never
	Country (optional) Remember me
	Note: Please do not include anything you consider confidential or proprietary. Your message and contact information may be shared with the author of any specific Demonstration for which you give feedback, but will not otherwise be published or distributed. Privacy Policy »

RSS

Atom