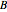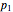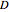Population Genetics: Hardy-Weinberg Equilibrium with Two Loci

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
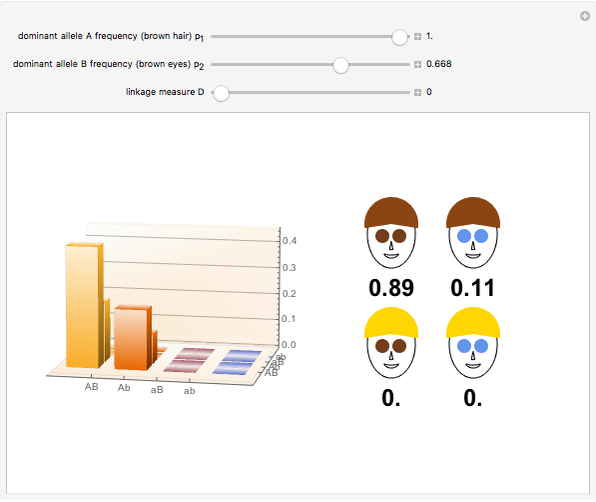
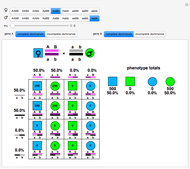
In population genetics, the distribution of genotypes and phenotypes in many instances follows a Hardy-Weinberg equilibrium. If 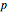 represents the frequency of a dominant allele
represents the frequency of a dominant allele  and
and 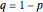 is the frequency of the corresponding recessive allele
is the frequency of the corresponding recessive allele  , the genotypes
, the genotypes 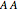 ,
,  , and
, and  occur in the ratios
occur in the ratios 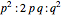 , persisting from generation to generation. Since both the homozygous phenotype
, persisting from generation to generation. Since both the homozygous phenotype 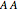 and the heterozygous (hybrid) phenotype
and the heterozygous (hybrid) phenotype  will exhibit the dominant trait, the fractional occurrence of the dominant and recessive traits occurs in the ratio
will exhibit the dominant trait, the fractional occurrence of the dominant and recessive traits occurs in the ratio  . Thus, contrary to some early misconceptions, a recessive trait can persist in a population. The principle was discovered independently by Wilhelm Weinberg, a German physician, and G. H. Hardy, the famous British mathematician (who took pride in the belief that none of his work would ever find practical application). Deviation from H–W equilibrium can be caused by one of several perturbing factors, including constrained mating, occurrence of mutations, random genetic drift, and natural selection.
. Thus, contrary to some early misconceptions, a recessive trait can persist in a population. The principle was discovered independently by Wilhelm Weinberg, a German physician, and G. H. Hardy, the famous British mathematician (who took pride in the belief that none of his work would ever find practical application). Deviation from H–W equilibrium can be caused by one of several perturbing factors, including constrained mating, occurrence of mutations, random genetic drift, and natural selection.
Contributed by: S. M. Blinder and Amy Blinder (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
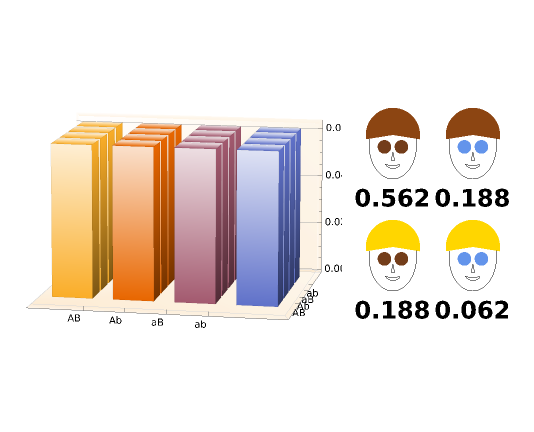
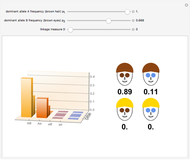
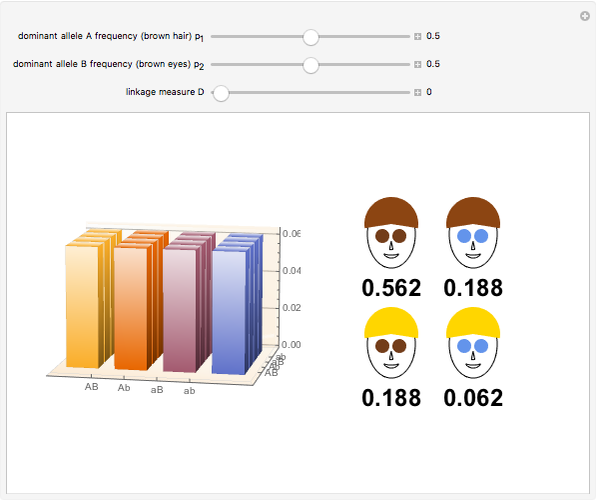
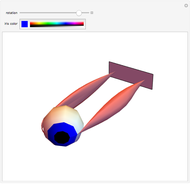
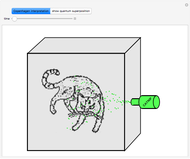
Snapshot 1: a single-locus Hardy-Weinberg distribution pertaining to eye color
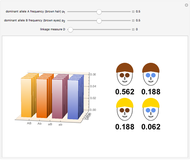
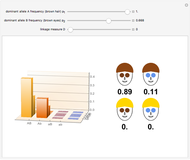
Snapshot 2: with equal genetic frequencies, a 9:3:3:1 distribution of phenotypes
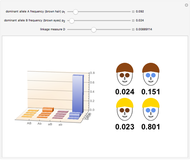
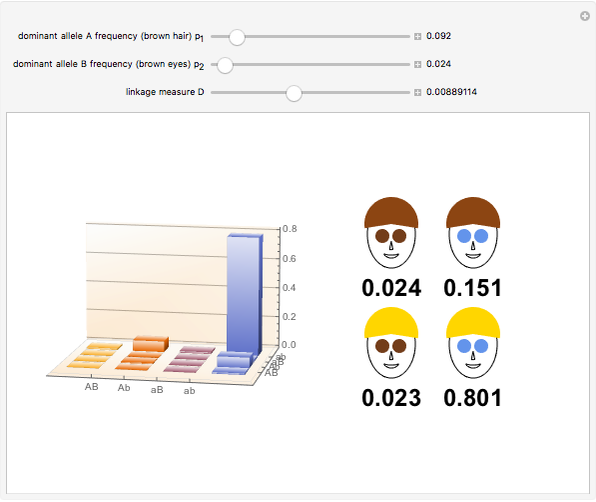
Snapshot 3: a possible haplotype distribution in central parts of Norway, Sweden, and Finland, where at least 80% of the population is blond and blue-eyed
References: Hardy-Weinberg Principle, Linkage Disequilibrium
Permanent Citation