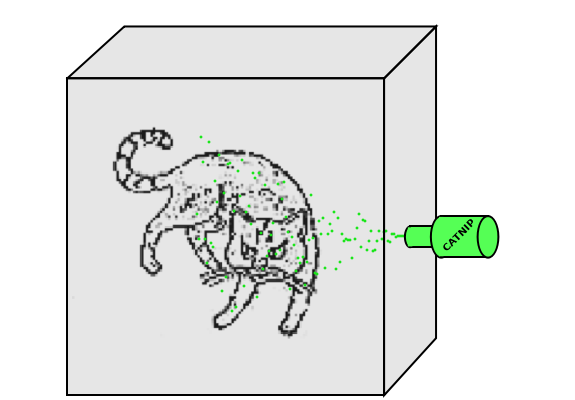
Schrödinger's Cat on Catnip

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
Schrödinger in 1935 proposed a gedankenexperiment questioning whether the worldview of the Copenhagen interpretation of quantum mechanics might apply also to phenomena on a macroscopic scale. In the version of the experiment described in this Demonstration, a cat is enclosed in an opaque box and a spray of catnip is released. Initially, the cat is in a perturbed state, resentful of being cooped up in a dark box. But, as the catnip begins to act, the cat will eventually relax into a blissful state. According to the Copenhagen interpretation, the time-dependent quantum state of the cat might be described by a wavefunction  , (
, ( ). However, the instantaneous state of the cat cannot be known until the box is opened, thus achieving a "reduction of the wavefunction" to one of two observable "pure" cat states,
). However, the instantaneous state of the cat cannot be known until the box is opened, thus achieving a "reduction of the wavefunction" to one of two observable "pure" cat states,  or
or  with probabilities
with probabilities  and
and  , respectively. In a sense, the state is "created" only after an actual measurement is made.
, respectively. In a sense, the state is "created" only after an actual measurement is made.
Contributed by: Sarah Blinder, Amy Blinder, and S. M. Blinder (November 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The superposition shown in the Thumbnail is purely conceptual.
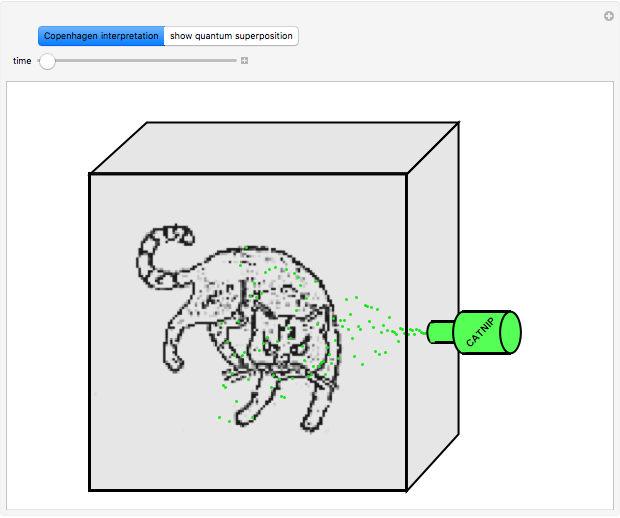
Snapshot 1: ready for experiment
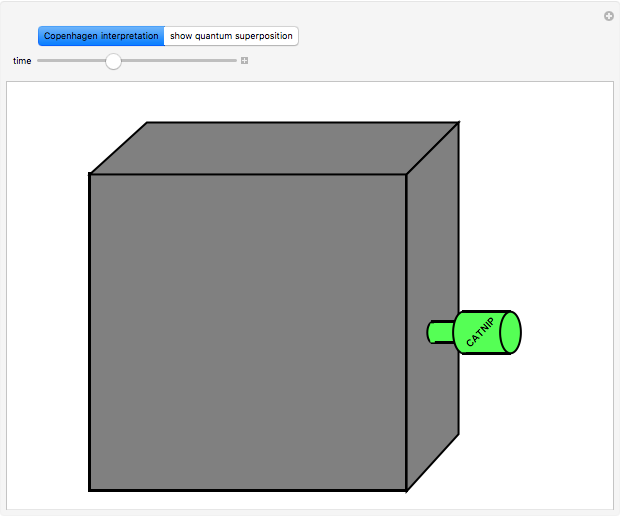
Snapshot 2: close box
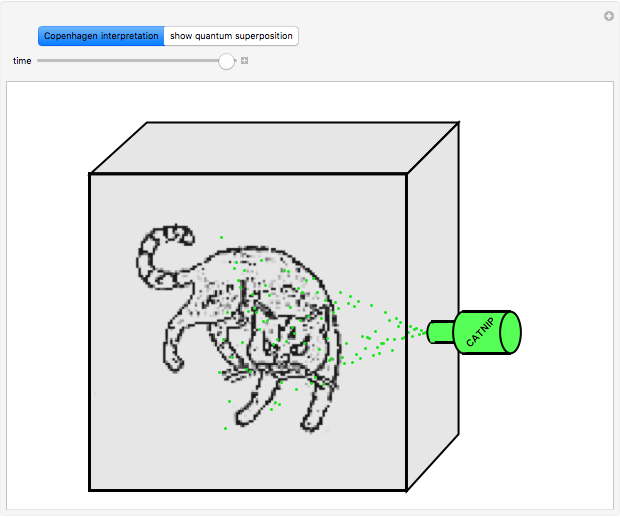
Snapshot 3: open box; one or the other pure state will be observed with a computable probability distribution
Schrödinger's original version proposed a cat enclosed in a box together with a hydrogen cyanide capsule that could be activated by a radioactive decay during a predetermined time interval. (It is suspected by some that Schrödinger's dog actually suggested the experiment.) The present, more humane, variant of the experiment was suggested by Sarah Blinder and Amy Blinder, referenced in [2].
References [1] S. M. Blinder, Introduction to Quantum Mechanics, Amsterdam: Elsevier, 2004 pp. 268–269. [2] S. M. Blinder, "A Kinder, Gentler Schrödinger Cat Experiment," American Journal of Physics, 69(6), 2001 pp. 633–634.
Permanent Citation