Cross Product in Spherical Coordinates

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
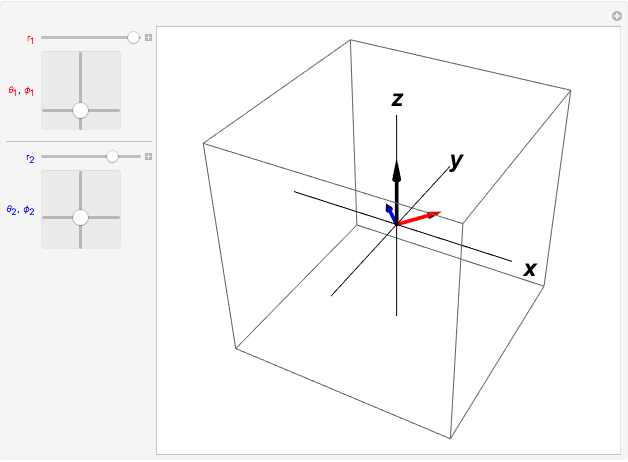
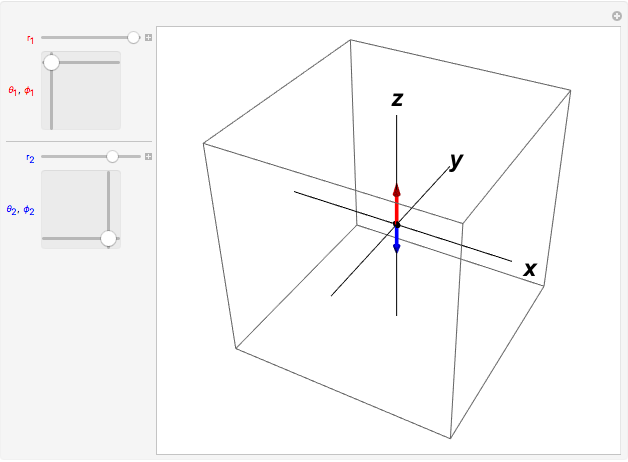
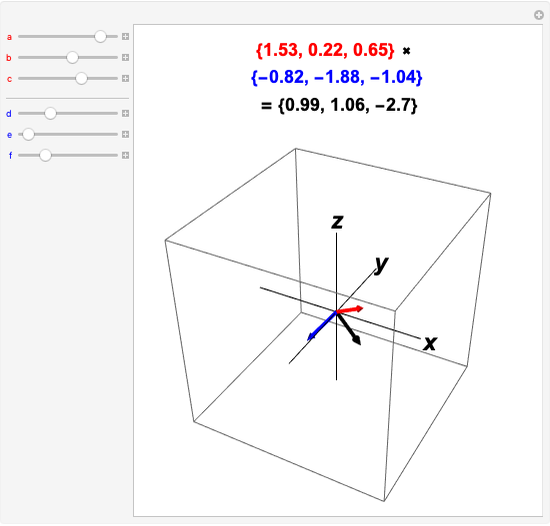
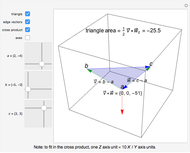
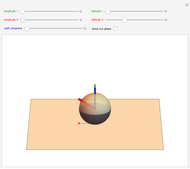
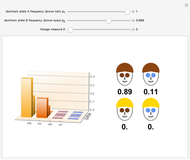
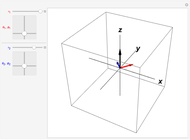
There is no simple formula for the cross product of vectors expressed in spherical polar coordinates. It is, however, possible to do the computations with Cartesian components and then convert the result back to spherical coordinates. This Demonstration enables you to input the vectors  and
and 
 then read out their product
then read out their product  , all expressed in spherical coordinates. The vectors are displayed at the bottom of the graphic, with the angles expressed as multiples of
, all expressed in spherical coordinates. The vectors are displayed at the bottom of the graphic, with the angles expressed as multiples of  .
.
Contributed by: S. M. Blinder and Amy Blinder (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Snapshot 1: Setting 
 and
and  are in the
are in the  ,
,  plane and
plane and  has only a
has only a  -component.
-component.
Snapshot 2: This shows the Cartesian unit vector relationship  .
.
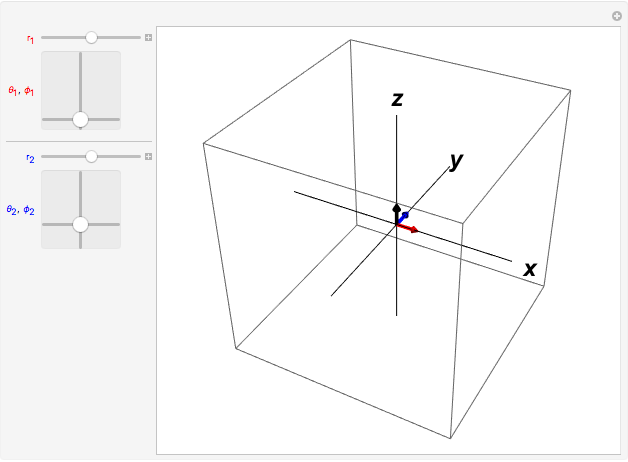
Snapshot 3: The vector product of two collinear vectors equals zero.
Permanent Citation