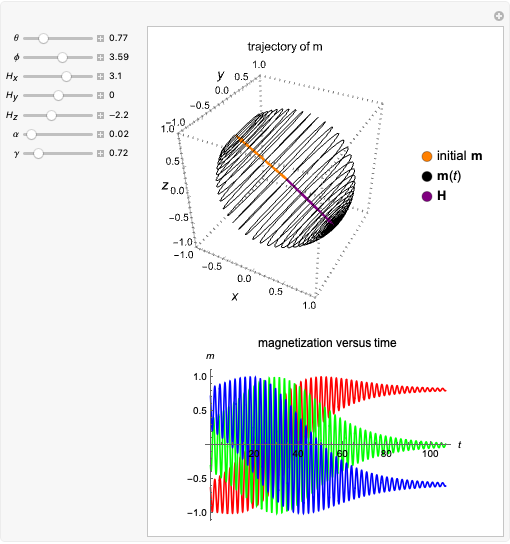
Precession of Magnetization Using the Landau-Lifshitz Equation

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
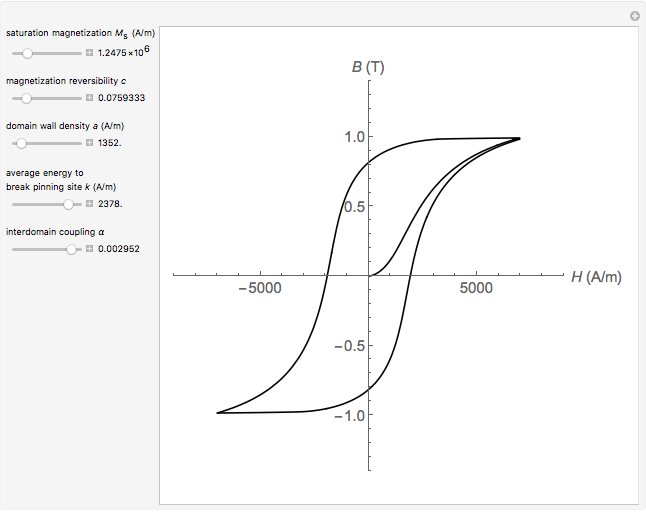
This Demonstration shows the time evolution of a single magnetization vector 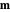 in an external magnetic field
in an external magnetic field 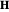 as governed by the Landau–Lifshitz equation. This simplified model features a precession term and a damping term. The precession term tends to rotate
as governed by the Landau–Lifshitz equation. This simplified model features a precession term and a damping term. The precession term tends to rotate 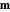 about
about 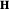 at a frequency proportional to the gyromagnetic ratio
at a frequency proportional to the gyromagnetic ratio 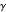 . The damping term dissipates energy from the system at a rate determined by
. The damping term dissipates energy from the system at a rate determined by 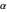 , as the magnetization vector approaches its low-energy configuration, aligned with
, as the magnetization vector approaches its low-energy configuration, aligned with 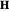 .
.
Contributed by: Danny Foster (August 27)
Open content licensed under CC BY-NC-SA
Details
The Landau–Lifshitz equation describes the magnetization dynamics of ferromagnetic materials within the framework of micromagnetism. The magnetization of a ferromagnetic material is modeled by a continuous vector field.
The results of micromagnetism operate best on nanometer length scales under the assumptions that the norm of the magnetization vector 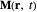 is equal to the saturation magnetization
is equal to the saturation magnetization 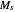 everywhere and that the energy functional
everywhere and that the energy functional 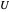 varies smoothly on atomic length scales.
varies smoothly on atomic length scales.
The dynamics of the system are closely tied to an effective field 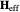 , which is defined as the functional derivative of the energy over the magnetization field:
, which is defined as the functional derivative of the energy over the magnetization field:
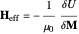 .
.
From this definition of the effective field, the Landau–Lifshitz equation can be written as:
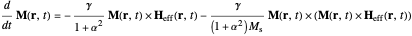 .
.
Again, 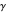 is the gyromagnetic ratio,
is the gyromagnetic ratio, 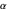 is the damping parameter, and
is the damping parameter, and 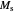 is the saturation magnetization. Some examples of common terms that contribute to
is the saturation magnetization. Some examples of common terms that contribute to 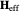 include the exchange field, the demagnetizing field and the external field. We are only considering the dynamics of a single magnetization vector in the presence of a uniform external field in this Demonstration. For simplicity, the saturation magnetization is fixed at 1, and the components can be changed by varying the polar angle
include the exchange field, the demagnetizing field and the external field. We are only considering the dynamics of a single magnetization vector in the presence of a uniform external field in this Demonstration. For simplicity, the saturation magnetization is fixed at 1, and the components can be changed by varying the polar angle  and the azimuthal angle
and the azimuthal angle  . The values of
. The values of  ,
, 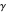 and each of the three Cartesian components of the field can also be varied.
and each of the three Cartesian components of the field can also be varied.
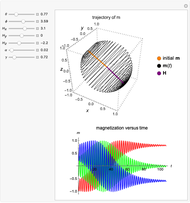
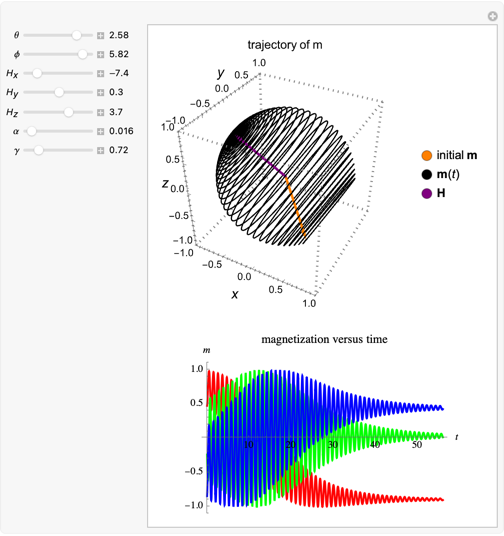
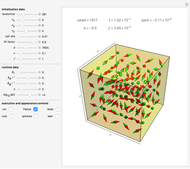
Snapshot 1: Using a small, nonzero 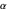 (
(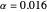 ),
), 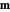 loses energy slowly as it relaxes toward the low-energy configuration. As a result,
loses energy slowly as it relaxes toward the low-energy configuration. As a result, 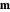 precesses around
precesses around 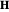 many times, and the trajectory resembles a tightly wound spiral.
many times, and the trajectory resembles a tightly wound spiral.
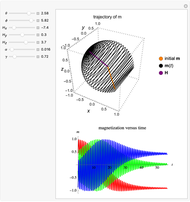
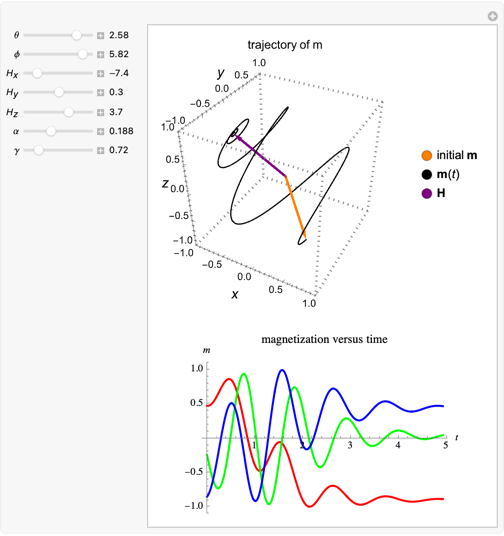
Snapshot 2: Here a larger value of 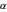 (
(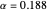 ) is used.
) is used. 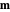 loses energy more quickly as it relaxes toward the low-energy configuration. As a result,
loses energy more quickly as it relaxes toward the low-energy configuration. As a result, 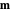 does not precess around
does not precess around 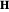 as many times, and the trajectory resembles a loosely wound spiral.
as many times, and the trajectory resembles a loosely wound spiral.
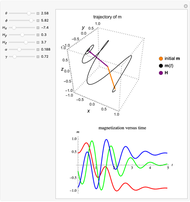
Snapshot 3: Setting the initial magnetization direction opposite of the external field direction, the energy of the system is maximized. However, 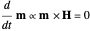 , so the configuration is stable. Likewise, as
, so the configuration is stable. Likewise, as  when the initial magnetization is in its lowest energy configuration, the lowest energy configuration is also stable.
when the initial magnetization is in its lowest energy configuration, the lowest energy configuration is also stable.
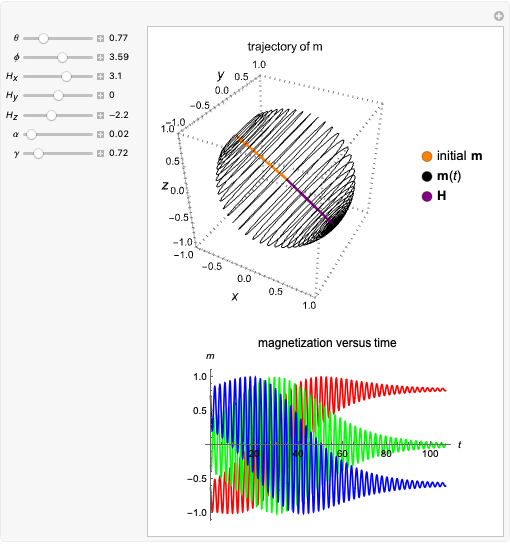
Snapshot 4: The system is placed in a configuration with 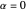 and
and  . The system does not lose energy, and the magnetization precesses around the external field.
. The system does not lose energy, and the magnetization precesses around the external field.
References
[1] L. Landau and E. Lifshitz, "On the Theory of the Dispersion of Magnetic Permeability in Ferromagnetic Bodies," Physikalische Zeitschrift der Sowjetunion, 8, Part 2, 1935 pp. 153–164. doi:10.1016/B978-0-08-036364-6.50008-9.
[2] J. M. D. Coey, Magnetism and Magnetic Materials, Cambridge: Cambridge University Press, 2010.
[3] C. Abert. "Micromagnetism." (Jun 13, 2023) micromagnetics.org/micromagnetism.
Snapshots
Permanent Citation