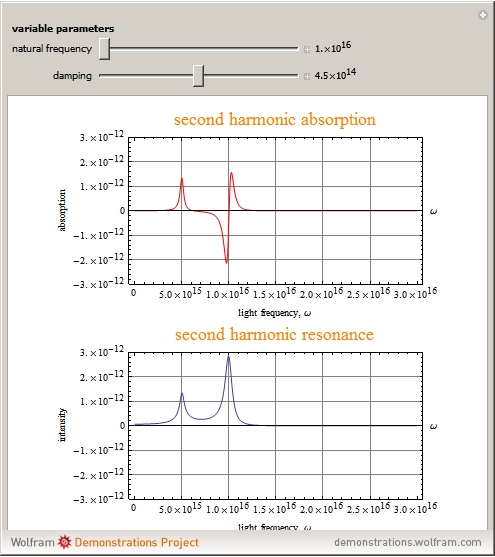
Second Harmonic Generation and Absorption Spectra

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
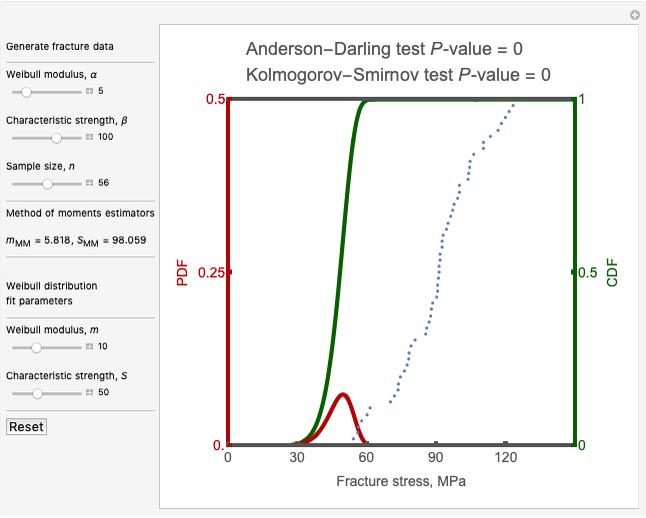
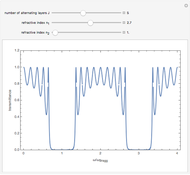
Light of frequency  shining on a nonlinear material can generate, in addition to the fundamental frequency
shining on a nonlinear material can generate, in addition to the fundamental frequency  , higher harmonics of frequencies
, higher harmonics of frequencies 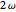 ,
,  ,
,  , and so on. If the material is noncentrosymmetric, the dipoles produced by the valence electronic motion driven by the nonlinear polarization can produce even-order harmonic generation. The simplest even harmonic generation has double the fundamental frequency of
, and so on. If the material is noncentrosymmetric, the dipoles produced by the valence electronic motion driven by the nonlinear polarization can produce even-order harmonic generation. The simplest even harmonic generation has double the fundamental frequency of  and is known as second harmonic generation (SHG).
and is known as second harmonic generation (SHG).
Contributed by: Hendradi Hardhienata (May 2014)
(Center for Surface and Nanoanalytics, JKU, Linz, Austria and Department of Physics, Bogor Agricultural University)
Idea suggested by: Kurt Hingerl
(Center for Surface and Nanoanalytics, JKU, Linz, Austria)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The linear and second-harmonic susceptibility can be calculated from the one-dimensional anharmonic Lorentz model:
 ,
,
where  is the displacement of the electron,
is the displacement of the electron, 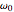 is the fundamental frequency of the system,
is the fundamental frequency of the system,  is the electronic charge,
is the electronic charge,  is the damping constant,
is the damping constant,  is the electron mass,
is the electron mass,  is the driving field, and
is the driving field, and  is the nonlinear coefficient given by
is the nonlinear coefficient given by
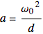 ,
,
where  is the lattice constant. Solving the model using an approximation method similar to the Rayleigh–Schrödinger perturbation theory gives the linear susceptibility
is the lattice constant. Solving the model using an approximation method similar to the Rayleigh–Schrödinger perturbation theory gives the linear susceptibility
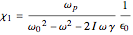
and the second harmonic susceptibility
 ,
,
where
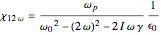
is the linear susceptibility for the frequency  .
.
For a step-by-step derivation of the formulas, see [1].
Here
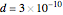 ,
,
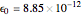 , the vacuum permittivity,
, the vacuum permittivity,
 ,
,
 ,
,
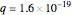 ,
,
 ,
,
 ,
,
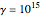 .
.
The absorption curve can be obtained from 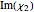 . Although not shown here, the real SHG susceptibility can simply be obtained using
. Although not shown here, the real SHG susceptibility can simply be obtained using  . The real linear and SHG susceptibility does not violate causality because it is consistent with the Kramers–Kronig relation. This is, however, not always the case in nonlinear optics, especially in time-resolved spectroscopy involving pump-probe input (e.g. four-wave mixing), where when coming into the nonlinear material, the pump signal precedes the probe signal, or in processes where the probe produces self-induced absorption on the material. More on this can be found in [2].
. The real linear and SHG susceptibility does not violate causality because it is consistent with the Kramers–Kronig relation. This is, however, not always the case in nonlinear optics, especially in time-resolved spectroscopy involving pump-probe input (e.g. four-wave mixing), where when coming into the nonlinear material, the pump signal precedes the probe signal, or in processes where the probe produces self-induced absorption on the material. More on this can be found in [2].
References
[1] R. W. Boyd, Nonlinear Optics, 2nd ed., San Diego: Academic Press, 2003.
[2] V. Lucarini, J. J. Saarinen, K.-E. Peiponen, E.-M. Vartiainen, Kramers-Kronig Relations in Optical Materials Research, New York: Springer, 2005.
Permanent Citation