Drude-Lorentz Model for Dispersion in Dielectrics

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
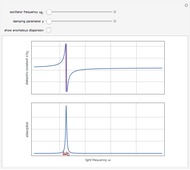
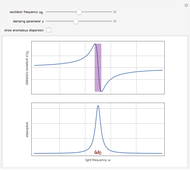
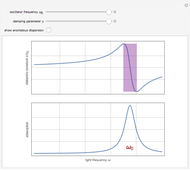
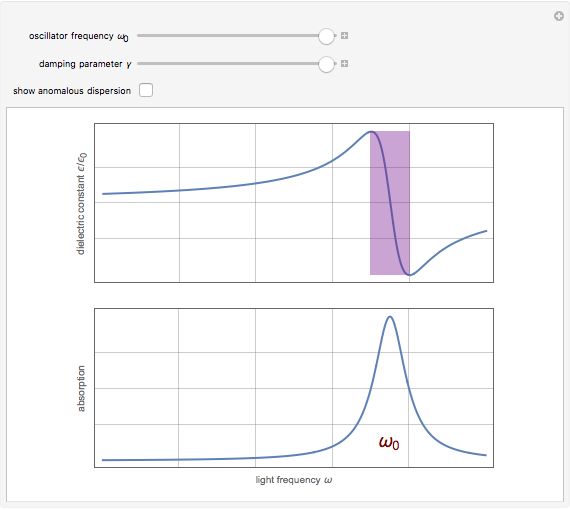
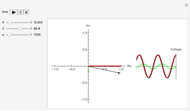
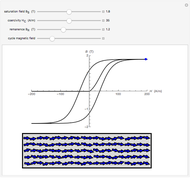
Drude and Lorentz (ca. 1900) developed a classical theory to account for the complex index of refraction and dielectric constant of materials, as well as their variations with the frequency of light. The model is based on treating electrons as damped harmonically bound particles subject to external electric fields. A highly simplified version of the model is given in this Demonstration, with results limited to a qualitative level. Still, the phenomena of normal and anomalous dispersion and their relation to the absorption of radiation can be quite reasonably accounted for. The classical parameters of the theory transform simply to their quantum analogs, so that the results remain valid in modern theories of materials science.
[more]
Contributed by: S. M. Blinder (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The equation of motion for a harmonically bound classical electron interacting with an electric field  is given by the Drude–Lorentz equation
is given by the Drude–Lorentz equation 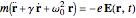 , where
, where  is the natural frequency of the oscillator and
is the natural frequency of the oscillator and  is the damping constant. For an incident electromagnetic field of frequency
is the damping constant. For an incident electromagnetic field of frequency  ,
, 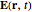 at the point
at the point  can be conveniently represented by a complex exponential
can be conveniently represented by a complex exponential 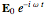 . The steady-state solution, in complex form, is given by
. The steady-state solution, in complex form, is given by 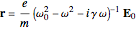 . The electric dipole moment of the electron,
. The electric dipole moment of the electron,  , corresponds to the macroscopic relation for the polarizability
, corresponds to the macroscopic relation for the polarizability 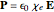 , where
, where 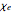 is the complex electric susceptibility
is the complex electric susceptibility 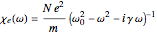 ,
, 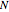 being the number of polarizable electrons per unit volume. It is sufficient to approximate
being the number of polarizable electrons per unit volume. It is sufficient to approximate 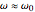 , with transition frequencies lying in the optical region
, with transition frequencies lying in the optical region 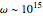 rad/s. Also,
rad/s. Also,  . The real part of the susceptibility
. The real part of the susceptibility 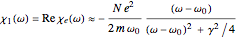 gives the frequency dependence (dispersion) of the dielectric constant
gives the frequency dependence (dispersion) of the dielectric constant 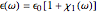 and index of refraction
and index of refraction 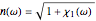 . The imaginary part
. The imaginary part 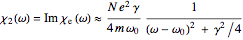 represents the absorption coefficient. This function has the form of a Lorentzian.
represents the absorption coefficient. This function has the form of a Lorentzian.
In the more accurate quantum theory of dispersion, the frequency  is replaced by a sum over several atomic transition frequencies and the damping parameters
is replaced by a sum over several atomic transition frequencies and the damping parameters  are determined by excited-state lifetimes.
are determined by excited-state lifetimes.
The real and imaginary parts of the susceptibility are connected by the Kramers–Kronig relations: 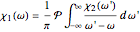 and
and 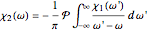 , where
, where  signifies the Cauchy principal value of the integral.
signifies the Cauchy principal value of the integral.
Reference
[1] L. Rosenfeld, Theory of Electrons, New York: Dover Publications, 1965, pp. 68 ff.
Permanent Citation