Primitive Elements in the Free Group of Rank Two

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
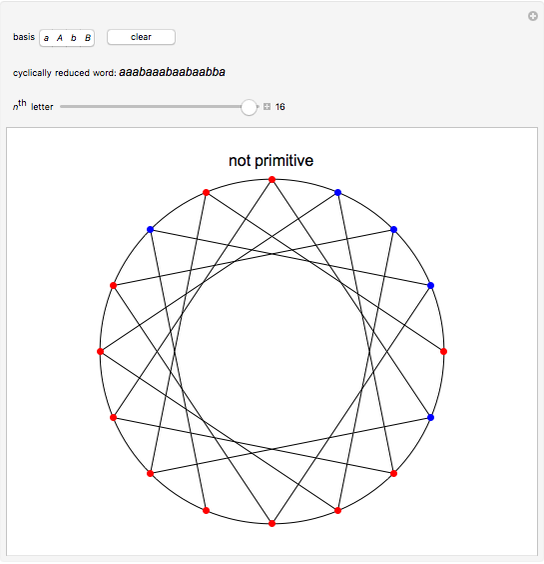
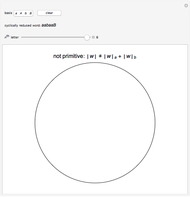
This Demonstration determines whether or not a word in the free group of rank two is primitive. Let 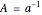 and
and 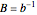 . The word is first cyclically reduced, that is,
. The word is first cyclically reduced, that is, 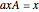 and so on. If it contains both
and so on. If it contains both  and
and  or
or  and
and  , then the word is not primitive. Otherwise, the word is written along the unit circle moving
, then the word is not primitive. Otherwise, the word is written along the unit circle moving 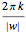 between letters, where
between letters, where 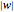 is the length of the word and
is the length of the word and  , where
, where 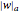 and
and 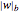 are the absolute values of the exponent sums of
are the absolute values of the exponent sums of  and
and  , respectively. A red disk indicates
, respectively. A red disk indicates 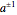 and a blue disk indicates
and a blue disk indicates 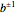 . If either of the two letters occupy the same location on the circle, or if the letters are not in two contiguous groups, the element is not primitive.
. If either of the two letters occupy the same location on the circle, or if the letters are not in two contiguous groups, the element is not primitive.
Contributed by: Matt Clay (June 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
An element in a free group is primitive if there exists a basis for the free group containing the given element. For free groups of rank two, Piggott observed that there is a very fast algorithm (linear on word length) that determines whether or not an element is primitive based on a construction by Osbourne and Zieschang. The algorithm to determine if a cyclic word 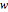 in the free group of rank 2 is as follows.
in the free group of rank 2 is as follows.
By 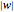 we denote the length of the word
we denote the length of the word 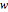 . By
. By 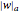 we denote the absolute value of the exponent sum of
we denote the absolute value of the exponent sum of  . In other words, the absolute value of the number of
. In other words, the absolute value of the number of  ’s minus the number of
’s minus the number of  ’s. We define
’s. We define 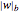 similarly.
similarly.
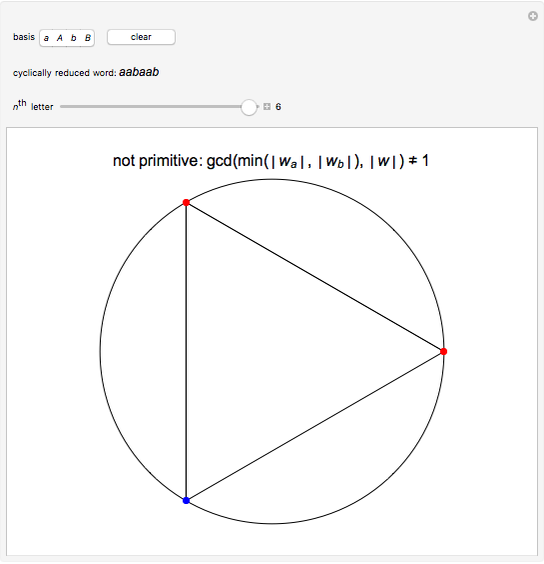
1. If both  and
and  appear in
appear in  or if both
or if both  and
and  appear, then
appear, then  is not primitive. This happens precisely when
is not primitive. This happens precisely when 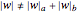 .
.
2. If 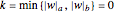 , then
, then 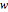 is primitive if and only if
is primitive if and only if 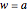 or
or 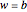 , i.e.,
, i.e., 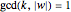 .
.
3. Otherwise, 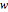 is written cyclically around the unit circle starting at the point
is written cyclically around the unit circle starting at the point 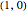 and moving
and moving 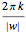 between letters. If two letters occupy the same location on the circle, i.e.,
between letters. If two letters occupy the same location on the circle, i.e., 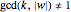 , or if the two letters are not in two contiguous groups, the element is not primitive. If these two conditions do not occur, then the word is primitive.
, or if the two letters are not in two contiguous groups, the element is not primitive. If these two conditions do not occur, then the word is primitive.
Inverses of basis elements are denoted by capital letters: 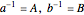 , etc.
, etc.
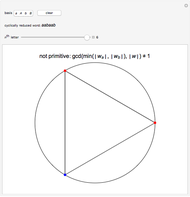
Snapshot 1: The word  is not primitive as both
is not primitive as both  and
and  appear, i.e.,
appear, i.e., 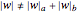 . For this word,
. For this word, 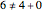 .
.
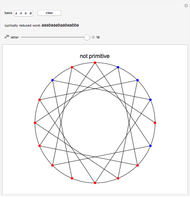
Snapshot 3: The word 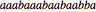 is not primitive as the groups of letters are not contiguous.
is not primitive as the groups of letters are not contiguous.
A C implementation of this algorithm can be obtained from Piggott’s website.
References
[1] R. P. Osborne and H. Zieschang, "Primitives in the Free Group on Two Generators," Inventiones Mathematicae, 63(1), 1981 pp. 17–24.
[2] A. Piggott, "Palindromic Primitives and Palindromic Bases in the Free Group of Rank Two," Journal of Algebra, 304(1), 2006 pp. 359–366.
Permanent Citation