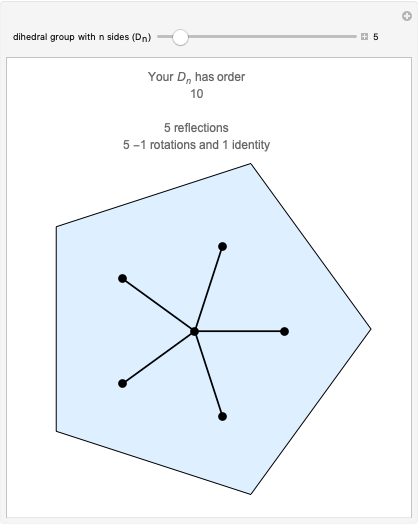
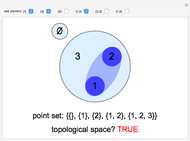
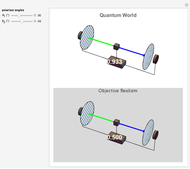
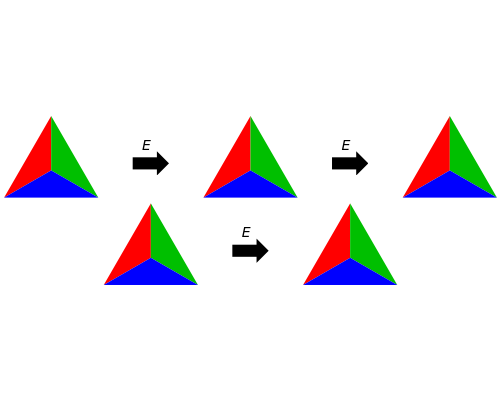C3v Group Operations

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
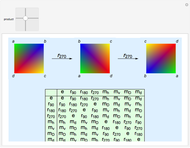
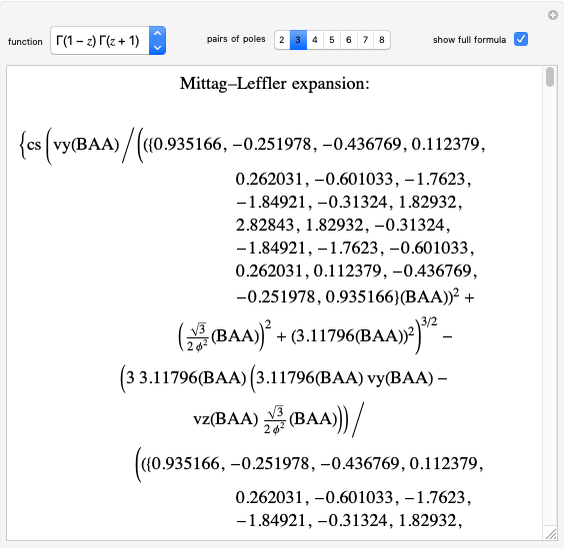
The sliders for operations 1, 2, and 3 perform actions of the symmetry group  , as indicated by labels above the three arrows. The group
, as indicated by labels above the three arrows. The group  is isomorphic with the symmetric group
is isomorphic with the symmetric group  and the dihedral group
and the dihedral group  . You can explore the results of applying successive operations 1 and 2 of the symmetry group
. You can explore the results of applying successive operations 1 and 2 of the symmetry group  , using tricolored equilateral triangles. The same result can be obtained in a single step using some operation 3. For example, the operation
, using tricolored equilateral triangles. The same result can be obtained in a single step using some operation 3. For example, the operation  followed by
followed by  gives the same result as the operation
gives the same result as the operation  . In standard group theory notation, this is written right-to-left as the symbolic product
. In standard group theory notation, this is written right-to-left as the symbolic product  . Note that
. Note that  , showing that symmetry operations do not, in general, commute.
, showing that symmetry operations do not, in general, commute.
Contributed by: S. M. Blinder (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
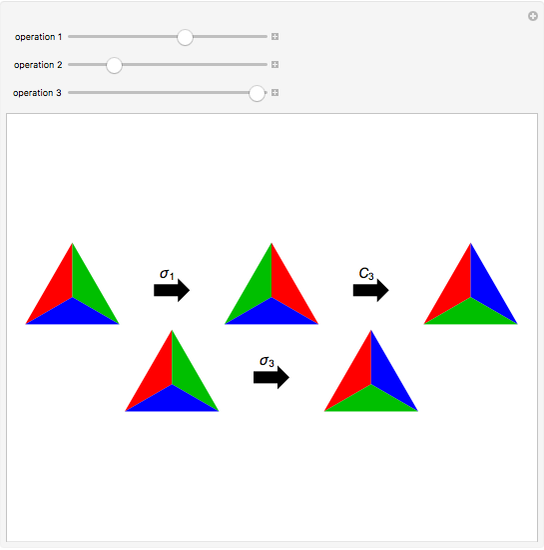
Snapshot 1: the group operations designated 
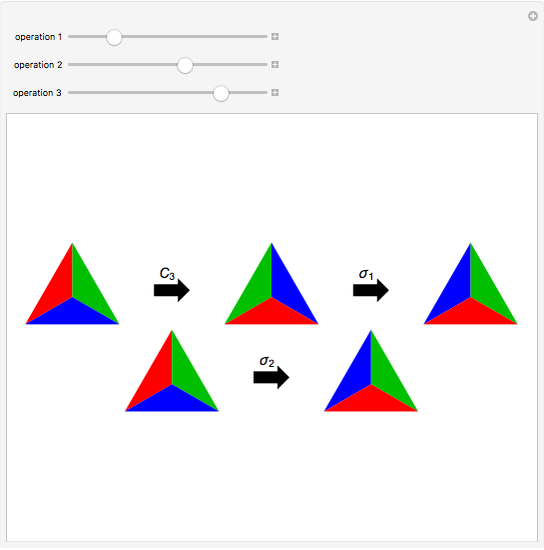
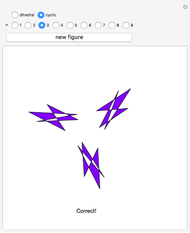
Snapshot 2:  , showing noncommutativity of group operations
, showing noncommutativity of group operations
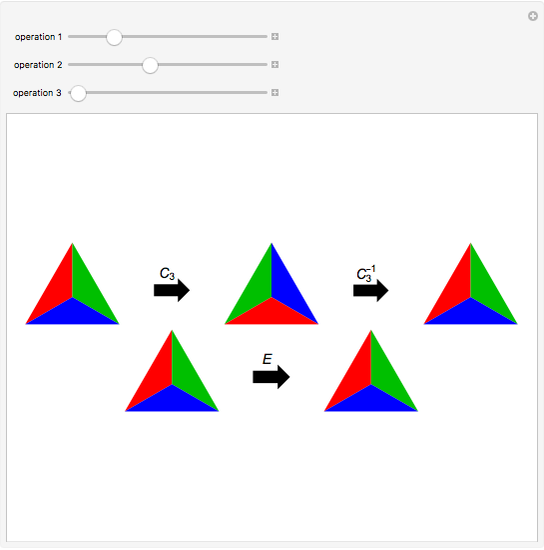
Snapshot 3: every element has an inverse
Permanent Citation