Reversible and Irreversible Expansion and Compression Processes

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
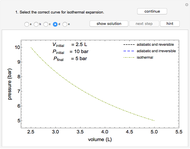
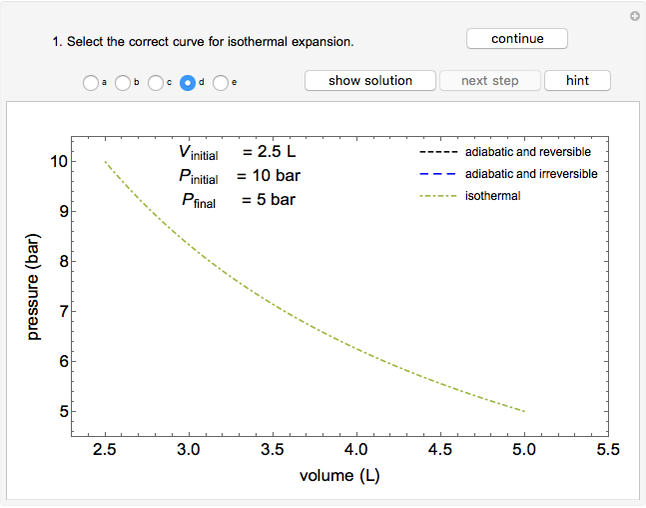
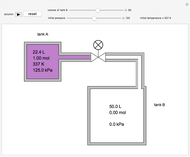
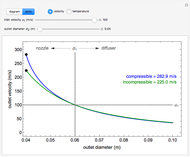
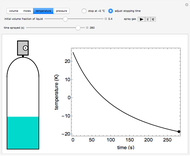
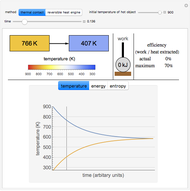
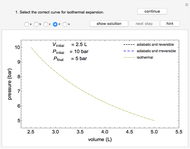
Use this Demonstration to identify isothermal, reversible-adiabatic and irreversible-adiabatic processes of an ideal gas in a step-by-step procedure. After starting and with "new problem" selected, the Demonstration shows either an expansion or a compression process, and either a pressure-temperature or pressure-volume diagram. Select your answer from the possible options (a, b, c, d, e) and then select "show solution" to see the correct answer. The "hint" button provides a hint for each step, and once "show solution" is selected, you cannot go back.
Contributed by: Neil C. Hendren (March 2011)
Additional contributions by: John L. Falconer and Rachael L. Baumann
(University of Colorado Boulder, Department of Chemical and Biological Engineering)
Open content licensed under CC BY-NC-SA
Details
The first law of thermodynamics, representing the conservation of energy, is:
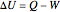 ,
,
where  is the change to internal energy of the system,
is the change to internal energy of the system, 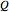 is heat added to the system and
is heat added to the system and 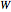 is the work done by the system. In adiabatic processes,
is the work done by the system. In adiabatic processes, 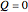 , while
, while 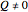 in isothermal processes with external pressure
in isothermal processes with external pressure 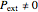 . Expansion-compression work
. Expansion-compression work 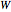 for all four processes is calculated from:
for all four processes is calculated from:
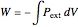 ,
,
where 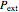 is the external pressure and
is the external pressure and 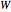 is in units of kJ/mol. The external pressure and the gas pressure are equal for a reversible process, whereas for an irreversible process the external pressure is equal to the final pressure. Change in internal energy is calculated from:
is in units of kJ/mol. The external pressure and the gas pressure are equal for a reversible process, whereas for an irreversible process the external pressure is equal to the final pressure. Change in internal energy is calculated from:
 .
.
Initial state:
 ,
,
where the subscript  refers to the initial state,
refers to the initial state, 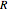 is the ideal gas constant (kJ/mol K),
is the ideal gas constant (kJ/mol K), 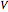 is volume (
is volume (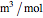 ),
), 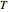 is temperature (K) and
is temperature (K) and 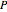 is pressure (Pa).
is pressure (Pa).
For an isothermal process:
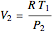 ,
,
where the subscript  refers to the final condition.
refers to the final condition.
Reversible work:
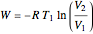 .
.
Irreversible work:
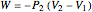 .
.
For an adiabatic process on an ideal diatomic gas:
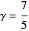 ,
,
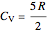 ,
,
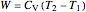 ,
,
where 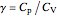 ,
, 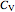 is the constant volume heat capacity and
is the constant volume heat capacity and 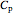 is the constant pressure heat capacity (kJ/(mol K)).
is the constant pressure heat capacity (kJ/(mol K)).
Reversible process:
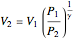 ,
,
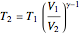 .
.
Irreversible process:
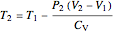 ,
,
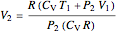 .
.
Reference
[1] J. R. Elliott and C. T. Lira, Introductory Chemical Engineering Thermodynamics, 2nd ed., Upper Saddle River, NJ: Prentice Hall, 2012.
Snapshots
Permanent Citation