Vapor-Liquid-Liquid Equilibrium (VLLE)

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
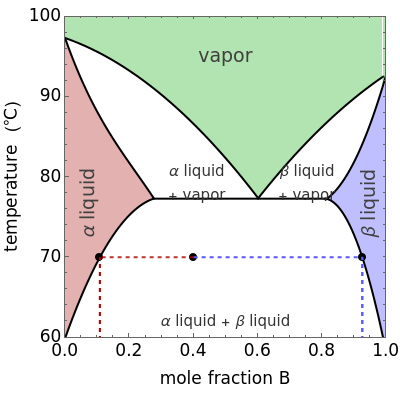
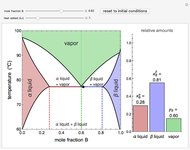
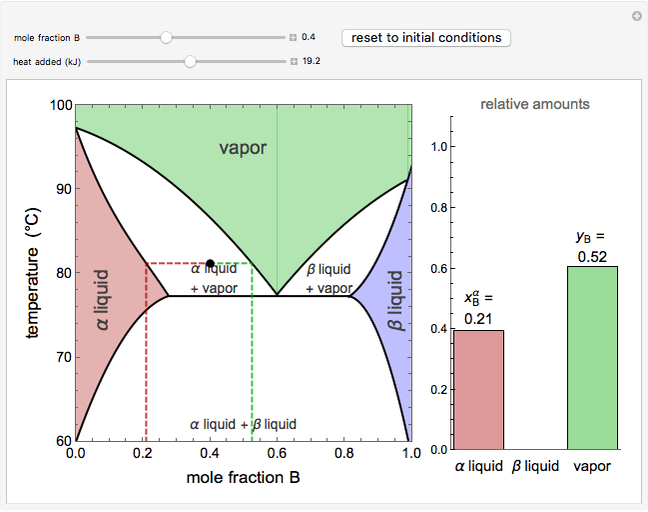
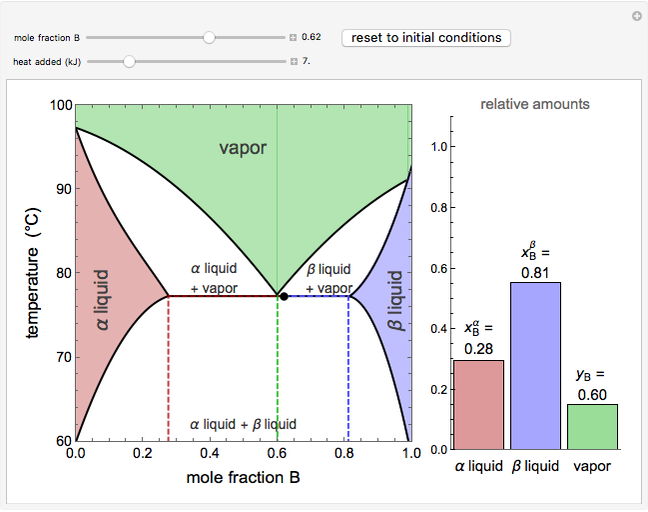
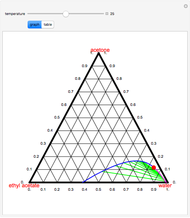
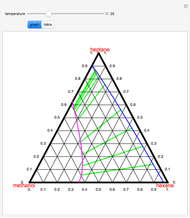
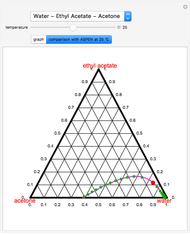
This Demonstration shows phase equilibrium for a binary system of two partially miscible liquids, A and B. Because of the partial miscibility, vapor-liquid equilibrium (VLE), liquid-liquid equilibrium (LLE), and vapor-liquid-liquid equilibrium (VLLE) are present on the phase diagram. You can vary the mole fraction of component B and the heat added (location of the black dot). The heat added changes the temperature, except when at 77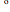 C, where all three phases are in equilibrium:
C, where all three phases are in equilibrium:  liquid (
liquid (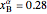 ),
), 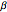 liquid (
liquid (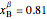 ), and vapor (
), and vapor (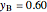 ). At this temperature, one phase must completely evaporate (or condense if removing heat) before the temperature increases (or decreases). The amount of heat added is used to illustrate the system behavior and to show how at 77
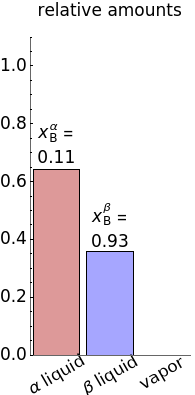
). At this temperature, one phase must completely evaporate (or condense if removing heat) before the temperature increases (or decreases). The amount of heat added is used to illustrate the system behavior and to show how at 77 C all three phases exist. The relative amounts of each phase are determined from the lever rule (mole balance) and are shown in the bar graph. The mole fraction(s) of component B in each phase are also displayed on the bar graph, for the phases present. In the multiple phase regions, dashed lines in the
C all three phases exist. The relative amounts of each phase are determined from the lever rule (mole balance) and are shown in the bar graph. The mole fraction(s) of component B in each phase are also displayed on the bar graph, for the phases present. In the multiple phase regions, dashed lines in the  diagram show what the mole fraction of B is where the vertical lines cross the
diagram show what the mole fraction of B is where the vertical lines cross the  axis.
axis.
Contributed by: Megan Maguire and Neil C. Hendren (August 2014)
With contributions by: John L. Falconerand Rachael L. Baumann
(University of Colorado Boulder, Department of Chemical and Biological Engineering)
Open content licensed under CC BY-NC-SA
Snapshots
Details
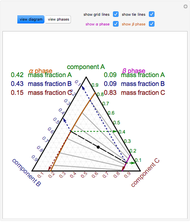
The relative amounts of each phase in the two-phase regions are found using the lever rule. An example of using the lever rule in the  liquid plus
liquid plus  liquid region is given by the following equations:
liquid region is given by the following equations:
relative amount of  liquid
liquid 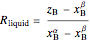 ,
,
relative amount of 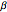 liquid
liquid  ,
,
where 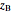 is the overall mole fraction of the mixture (the mole fraction of the point in the
is the overall mole fraction of the mixture (the mole fraction of the point in the  diagram).
diagram).
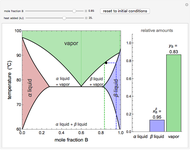
When the system is in vapor-liquid-liquid equilibrium, the relative amounts of each phase are found from mass balances. For example, using 10% vaporization and an initial mole fraction of B of 0.7 in the diagram:
• determine the initial mole fraction of B
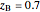
• determine the mole fraction of component B in each phase
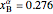 = mole fraction of B in the alpha phase
= mole fraction of B in the alpha phase
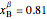 = mole fraction of B in the beta phase
= mole fraction of B in the beta phase
 = mole fraction of B in the vapor phase
= mole fraction of B in the vapor phase
• set a basis for the amount of total moles in the system
total moles = 1
• determine the percentage of vaporization
percent vaporization = 10%
• determine the amount of vapor in the system
 = (percent of vaporization) × (total moles) = 0.1 × 1 = 0.1
= (percent of vaporization) × (total moles) = 0.1 × 1 = 0.1
• perform a mole balance on the whole system
total moles = vapor +  liquid +
liquid +  liquid
liquid

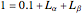
• perform a mole balance on component B
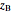 × total moles = (
× total moles = (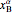 ×
× 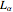 ) + (
) + (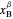 x
x 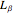 ) + (
) + ( x V)
x V)
0.7 × 1 = (0.276 × 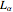 ) + (0.81 ×
) + (0.81 × 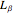 ) + (0.6 × 0.1)
) + (0.6 × 0.1)
0.7 = (0.276 × 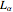 ) + (0.81 ×
) + (0.81 × 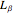 ) + 0.06
) + 0.06
• simultaneously solve the equations with unknown variables (the number of equations should equal the number of unknown variables)
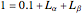
0.7 = (0.276 × 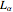 ) + (0.81 ×
) + (0.81 × 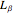 ) + 0.06
) + 0.06
• relative amounts of each phase
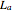 = 0.166 = relative amount of
= 0.166 = relative amount of  liquid phase
liquid phase
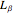 = 0.734 = relative amount of
= 0.734 = relative amount of 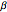 liquid phase
liquid phase
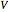 = 0.1 = relative amount of vapor
= 0.1 = relative amount of vapor
Permanent Citation