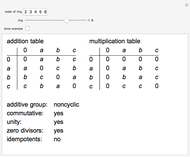
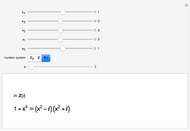Rings of Small Order

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
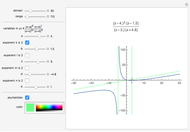
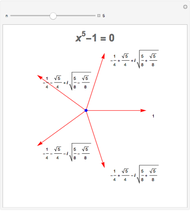
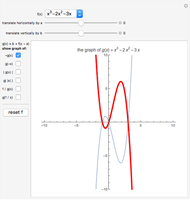
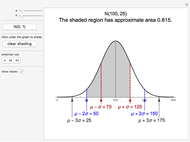
The addition and multiplication tables for all rings of order 2 through 6 are provided, along with a summary of some important facts about those rings. Each ring can be viewed as either an "abstract" ring or as a "concrete" example (matrices, polynomials, etc.); snapshots 1 and 2 show isomorphic rings, for example.
Contributed by: Marc Brodie (July 2011)
(Wheeling Jesuit University)
Open content licensed under CC BY-NC-SA
Snapshots
Details
There are only two rings of order  for a prime
for a prime  . There are 11 rings of order 4 and four rings of order 6. Since the additive group of a ring is Abelian, "commutative" refers to ring multiplication. A ring has unity if there is a multiplicative identity. A zero divisor is a nonzero ring element that can be multiplied by a nonzero ring element to get zero. For example, since
. There are 11 rings of order 4 and four rings of order 6. Since the additive group of a ring is Abelian, "commutative" refers to ring multiplication. A ring has unity if there is a multiplicative identity. A zero divisor is a nonzero ring element that can be multiplied by a nonzero ring element to get zero. For example, since  in
in  , both 2 and 3 are zero divisors in
, both 2 and 3 are zero divisors in  . A (nontrivial) idempotent is a nonzero, non-unity that is equal to its square. Since
. A (nontrivial) idempotent is a nonzero, non-unity that is equal to its square. Since  in
in  , 3 is an idempotent in
, 3 is an idempotent in  .
.
For more information, see "Small Rings".
Permanent Citation