Rogue Ocean Waves

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
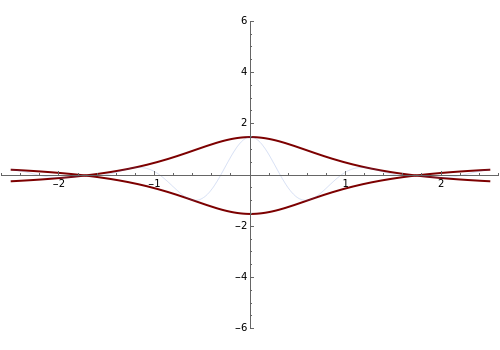
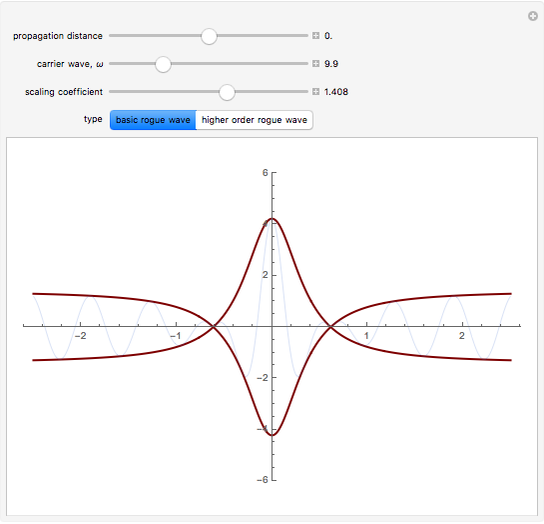
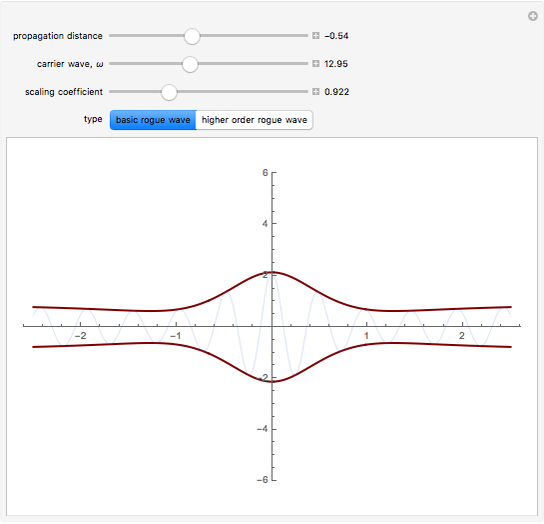
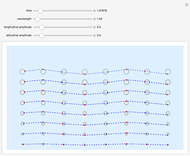
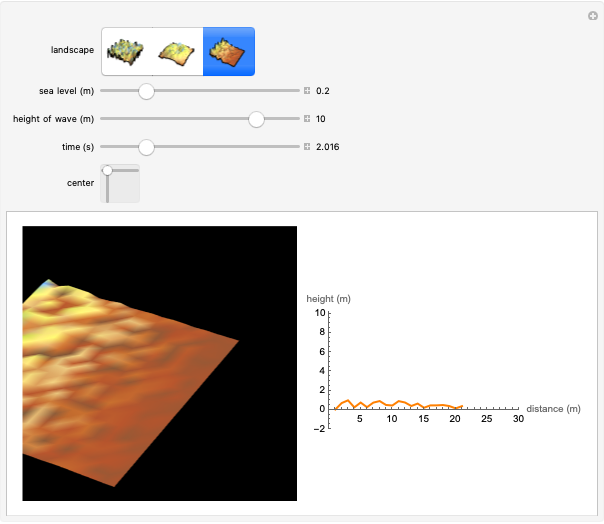
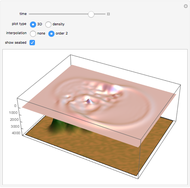
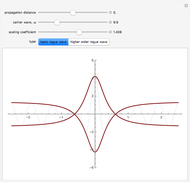
This Demonstration shows the formation of rogue (or freak) waves in the deep ocean, modeled using the well-known nonlinear Schrödinger equation, 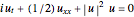 . The striking feature of this wave is that an almost flat ocean surface evolves into a singular wave with high amplitude, as energy is sucked into the center part of the wave from the surrounding area of the ocean.
. The striking feature of this wave is that an almost flat ocean surface evolves into a singular wave with high amplitude, as energy is sucked into the center part of the wave from the surrounding area of the ocean.
Contributed by: Adrian Ankiewicz (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
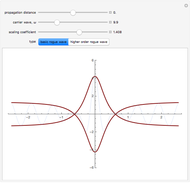
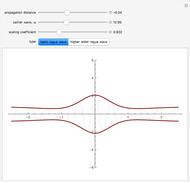
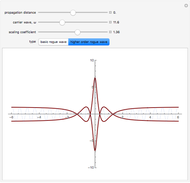
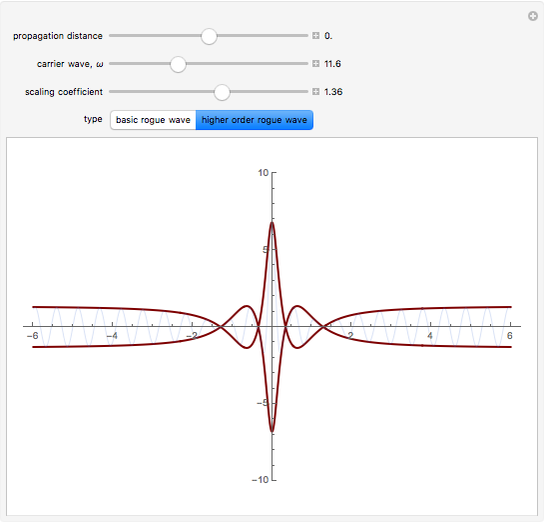
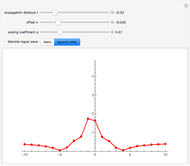
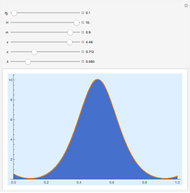
The process is highly nonlinear and may appear as a mystery to those who observe this rare event. Such destructive waves have sunk a number of ships in the ocean. Moreover, after its unexpected appearance, the big wave disappears, restoring the relatively peaceful surface of the ocean. Here, you can observe this unusual phenomenon, described by exact rational solutions of the nonlinear Schrödinger equation. There is a hierarchy of these solutions with progressively increasing amplitude. Only the two lowest order ones are presented here. You can switch from one to the other using the two buttons. The Demonstration allows you to change the distance of propagation and observe the sharp rise of the crest of the wave above the rest of the deep ocean when the distance along the ocean surface approaches zero. The second variable is the frequency of the carrier wave. It represents ripples that always exist on the ocean surface but do not directly influence the envelope of the rogue waves. The third parameter is a scaling factor that depends on a myriad of other physical parameters of the real ocean. It shows, in particular, that the wave crest can indeed be much higher than the rest of the waves around it. More details are given in N. Akhmediev, A. Ankiewicz, and M. Taki, "Waves That Appear from Nowhere and Disappear without a Trace," Phys. Lett. A, 373(6), 2009 pp. 675–678. For solitons, see http://wwwrsphysse.anu.edu.au/osc/
Permanent Citation
"Rogue Ocean Waves"
http://demonstrations.wolfram.com/RogueOceanWaves/
Wolfram Demonstrations Project
Published: March 7 2011