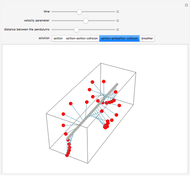
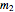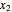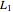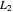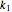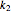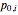Tuned Mass Damper System
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
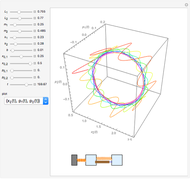
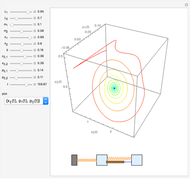
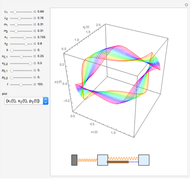
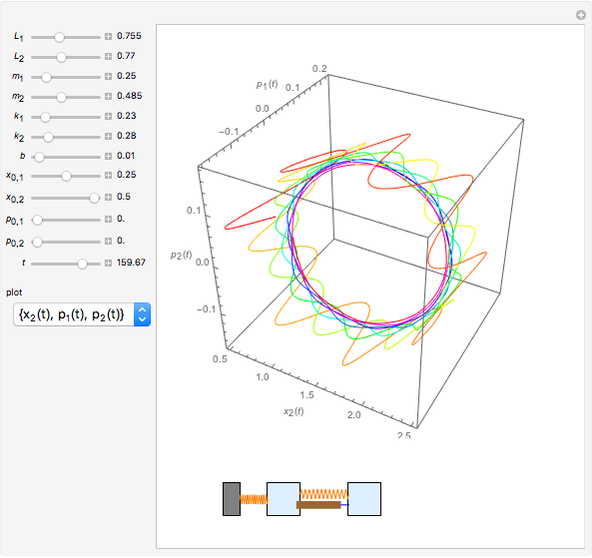
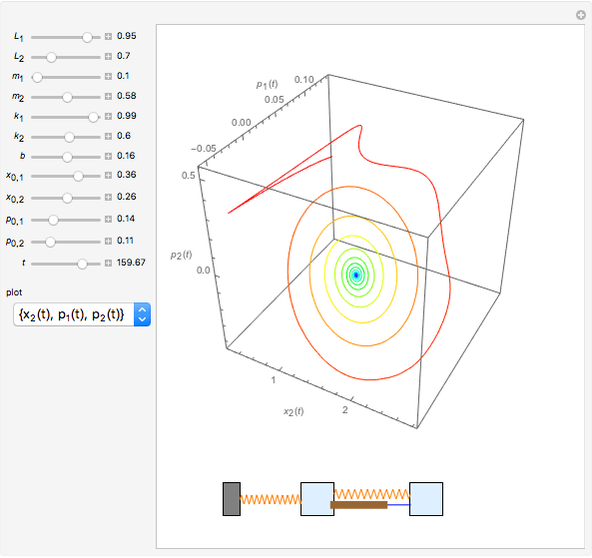
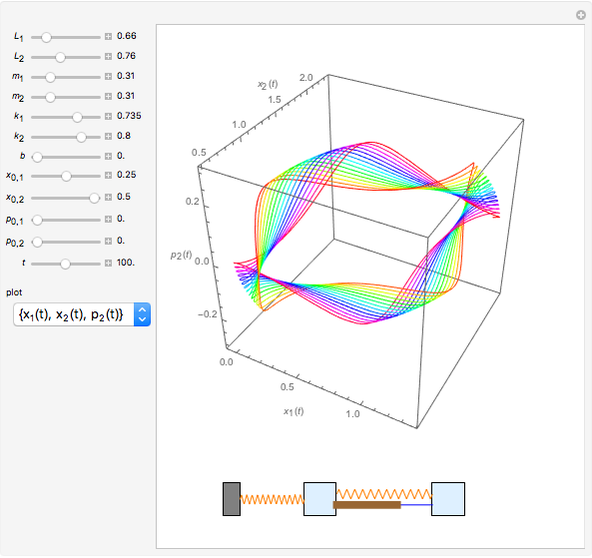
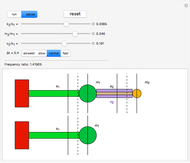
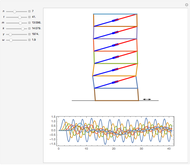
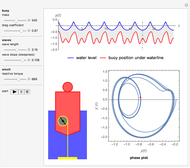
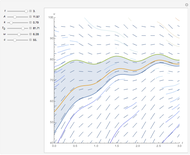
Tuned mass damper systems have been developed in recent years to diminish the oscillations of buildings during earthquakes. A large mass is hung by springs at the top of the building. The oscillations of the mass dissipates the energy into heat by means of a damper.
[more]
Contributed by: Enrique Zeleny (January 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The equations of motion are
 ,
,
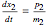 ,
,
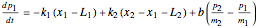 ,
,
 .
.
Reference
[1] P. Blanchard, R. L. Devaney, and G. R. Hall, Differential Equations, 4th ed., Boston: Brooks/Cole, 2012 pp. 515–519.
Permanent Citation